Dosing approaches

First dose

One approach is to use the population values for phenytoin. With this method we would use the population values of Vm = 7 mg/kg/day and Km = 5 mg/L. Aiming at 15 mg/L for with a patient weight of 80 kg, the equation

Equation XX-3 Dosing Rate versus Average Cp>

Probably better to start out low since toxicity is more probable above 20 mg/L.

Second dosing regimen

That is after giving a continuous dose regimen to steady state, measure plasma concentration and adjust dose. For example if after 420 mg/day, is 20 mg/L then a downward adjustment would be necessary. If we assume that the Km is close to the average value of 5 mg/L we can estimate Vm from the equation above

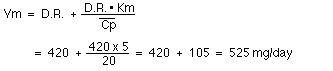
thus a new dose rate can be calculated

approximately 400 mg/day. Note: A reduction in dose of 20 mg/day (5 %) is calculated to give a 5 mg/L change (25 %) in . Another approach can be describe using the 'graph' (nomogram) shown below.

In Figure XX-6, Line A represents Cp^ss = 8 mg/L on 300 mg/day (70 kg = 4.3 mg/kg/day). Line B was drawn to achieve a new Cp^ss = 15 mg/L with a dose of 5.2 mg/kg/day (= 364 mg/day)

The graph is used by plotting the line described by the current Cp^ss and R on the graph, marking a point in the middle of the contour. From that point draw a line to the desired Cp^ss, the value on the vertical axis gives the required dose rate, R.

Figure 93, Nomogram for Phenytoin Dosing[3]

Third dosing regimen

If we already have two plasma concentrations after two dose rates we can solve the equation

using simultaneous equations.

With = 8.0 mg/L and = 27.0 mg/L for R1 = 225 mg/day and R2 = 300 mg/day

225 * Km + 225 * 8 = 8 * Vm (1)

and

300 * Km + 300 * 27 = 27 * Vm (2)

or multiplying (1) x 300

300 * 225 * Km + 300 * 225 * 8 = 300 * 8 * Vm (3)

and multiplying (2) x 225

300 * 225 * Km + 300 * 225 * 27 = 225 * 27 * Vm (4)

subtracting (4) - (3)

300 * 225 * (27 - 8) = (225 * 27 - 300 * 8) * Vm

and

With these Vm and Km values we can now calculate the next dosing regimen to try.

Graphical methods

There are a number of graphical methods which have been described for when you have data from more than two dosing intervals. Basically these rely on converting the equations mentioned above into a straight line form which can be plotted to give the Vm and Km as a function of the intercept and/or slope.

Copyright 2001 David W.A. Bourne