Another important property of first order kinetics is the half-life of elimination, t^1/2.

The half-life is the time taken for the plasma concentration to fall to half its original value. Thus if Cp = concentration at the start and Cp/2 is the concentration one half-life later then:-

ln 2 = kel * t1/2

or

OR

Note: Independent of concentration, a property of first order processes

These equations can be used as an approximate method of calculating kel. If we look at a plot of Cp versus time on semi-log graph paper.

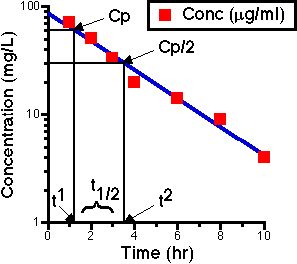
Figure IV-11. Semi-log Plot of Cp versus Time with Some Data and a Line

The steps to take

1) Draw a line through the points (this tends to average the data)

2) Pick any Cp and t¹

3) Determine Cp/2 and t²

4) Calculate t_1/2 as (t² - t¹)

Then kel = 0.693/t^1/2

Also consider determining Cp/4 or Cp/8 for two half-lives or three half-lives, respectively

The line smooths out the bumps. There may be bad data points, so by putting in a line you 'sort of' average the data. The half-life is the same whether going from 40 to 20 or from 10 to 5 mg/L. This is a property of the first order process.

Note:

Go from:

Cp - > Cp/2 in 1 half-life i.e. 50.0 % lost 50.0 %
Cp - > Cp/4 in 2 half-lives i.e. 25.0 % lost 75.0 %
Cp - > Cp/8 in 3 half-lives i.e. 12.5 % lost 87.5 %
Cp - > Cp/16 in 4 half-lives i.e. 6.25 % lost 93.75 %
Cp - > Cp/32 in 5 half-lives i.e. 3.125 % lost 96.875 %
Cp - > Cp/64 in 6 half-lives i.e. 1.563 % lost 98.438 %
Cp - > Cp/128 in 7 half-lives i.e. 0.781 % lost 99.219 %

Thus over 95 % lost or eliminated in 5 half-lives. Typically considered the completion (my definition unless told otherwise) of the process, although in theory it takes an infinite time. Others may wish to wait 7 half-lives where over 99% of the process is complete.

See Table IV-1 from earlier, for some typical half-life values.

Homework Set 1995

Copyright 2001 David W.A. Bourne