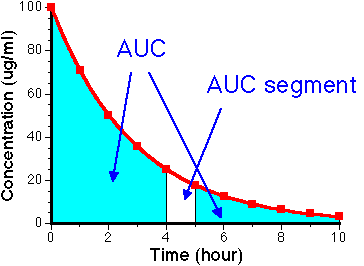
Figure IV-7. Linear Plot of Cp versus Time showing AUC and AUC segment

We can continue by looking at two more parameters. These are the area under the plasma concentration time curve (AUC) and the half-life of elimination. First AUC. The AUC value is very useful for calculating the relative efficiency of different drug products (We'll talk about this later). It will also give us another method of calculating the apparent volume of distribution, not just from Cp⁰.

The AUC is calculated by adding these segments together. Each very narrow segment has an area = Cp*dt. Thus the total area has the area, AUC.

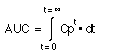
Equation IV-16. AUC for a Very Narrow Segment

calculus uses very narrow segments

then

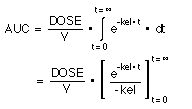
at t = 0, e^{- kel*t} = 1

at t = , e^{- kel*t} = 0

Therefore

or

Equation IV-17. AUC Calculated from Concentration and kel

Analytical integration (exact solution, given exact values for V and kel)

[Note: From t = 0 - > t = [[infinity]], AUC = Cp⁰/kel and for t = t - > t= [[infinity]] , AUC = Cp^t/kel]

or

Equation IV-18. Volume of Distribution Calculated from Dose, AUC and kel

We could use equation 20 to calculate the AUC value if we knew DOSE, kel, and V; but usually we don't and have to calculate AUC directly from the Cp versus time data.

We need then a different approach, which is called the trapezoidal rule. Numerical (approximate) solution

a) Trapezoidal rule

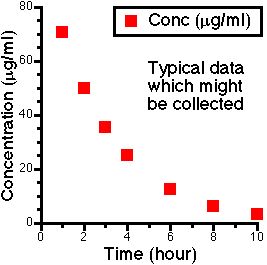
Figure IV-8. Linear Plot of Cp versus Time showing Typical Data Points

We can calculate the AUC of each segment if we consider the segments to be trapezoids. [Four sided figures with two parallel sides].

The area of each segment is then given by the average concentration x segment width.

See Figure IV-9 below

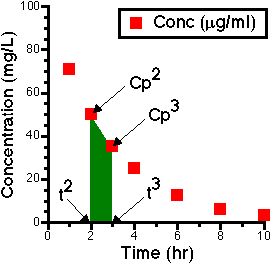
Figure IV-9. Linear Plot of Cp versus Time showing One Trapezoid

The area from the first to last data point can then be calculated by adding the areas together.

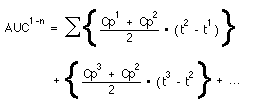
Note: Summation of data point information (non-calculus)

This gives:

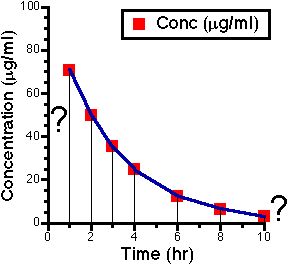
Figure IV-10. Linear plot of Cp versus time showing areas from data 1 to data n

We now have two more areas to consider. The first and the last.

First if we give a rapid I.V. bolus the zero plasma concentration Cp⁰ can be determined by extrapolation.

Thus

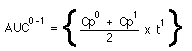
The final segment can be calculated if we go back to the mathematical equation.

can be derived

Therefore the total AUC can be calculated as :-

Table IV-4. Calculation of AUC

Time (hr)	Concentration (µg/ml)	delta AUC	AUC (µg.hr/ml)
0	100
1	71	85.5	85.5
2	50	60.5	146.0
3	35	42.5	188.5
4	25	30.0	218.5
6	12	37.0	255.5
8	6.2	18.2	273.7
10	3.1	9.3	283.0
Total		8.9	291.9

Copyright 2002 David W.A. Bourne