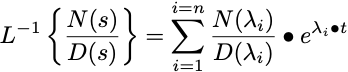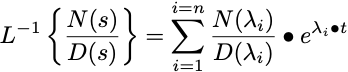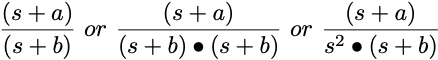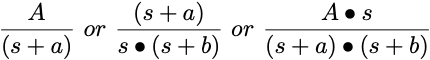Chapter 26
Integrating Differential Equations using Laplace Transforms
return to the Course index
previous | next
Finger Print Method
Inverse Laplace Transform
The so-called finger print method provides a quick and easy method for the back transformation of many of the Laplace equations found in pharmacokinetics. With a few limitations the method can be commonly applied. This method is derived from the explanation of the general partial fraction method presented by Benet and Turi (Benet, L.Z. and Turi, J.S. 1971. "Use of the General Partial Fraction Theorems for Obtaining Inverse Laplace Transforms in Pharmacokinetic Analysis", J. Pharm. Sci., 60: 1593-1594).
General Partial Fraction Method
The general partial fraction method is summarized with the equation:
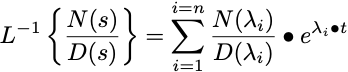
Equation 26.4.1 Equation demonstrating the General Partial Fraction Theorem
The function in 's' on the left is transformed into the function on the right in terms of 't' (time). The λ terms are the roots of the polynomial term in the denominator on the left. In pharmacokinetic equations these are usually zero or negative.
Limitations or Requirements
There are two requirements for this method to be applicable.
- The degree, in s, of the polynomial in the denominator must be higher than the polynomial in the numerator.
- There must be no repeating terms in the denominator
Examples
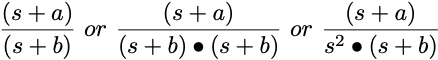
Equation 26.4.2 Fractions which Don't Comply with the Limitations
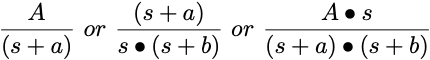
Equation 7.2.3 Fractions which Do Comply with the Limitations
General Procedure
The general procedure for this method is to:
- Check the Limitations of Requirements
- Determine the Roots in the Denominator
After solving for the Laplace of the amount or concentration of interest the denominator should be of the form:
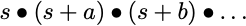
Equation 7.2.4 The General Form of the Denominator
In finding the root(s) of the polynomial in the denominator each of the factors can be set to zero and used to find a value (or root) for s. Thus, from Equation 7.2.4 the equations:
s = 0
s + a = 0
s + b = 0
...
can be written and the roots for the denominator are thus s = 0, s = -a, s = -b, etc.
- Write the back transform using the finger print method
There may be one or more roots to the denominator. The next step is to cover the part corresponding to each root in turn and replace all instances of 's' in the remaining equation with the current root. This term is then multiplied by eroot*t. The final result is the sum of all the terms from each root. Note: The roots for pharmacokinetic problems are usually negative (or zero) and thus the exponential term usually ends being negative.
- Simplify the result as necessary
This page was last modified: Sunday, 28th Jul 2024 at 5:08 pm
Privacy Statement - 25 May 2018
Material on this website should be used for Educational or Self-Study Purposes Only
Copyright © 2001 - 2025 David W. A. Bourne (david@boomer.org)
 | Name the Drug
A game to aid recognizing brand versus generic drug names
See how many names you can catch before you run out of lives |
|