Chapter 26 Integrating Differential Equations using Laplace Transforms

return to the Course index
previous | next

Convolution

The convolution method described by Benet (Benet, 1972) allows the development of the Laplace equation for the amount of drug in the central compartment by a simple multiplication of the input function and the disposition function. A ke/s function can be included to derive the amount of drug in urine. The input function describes the route of administration. The disposition function describes the first order distribution and elimination processes, and on this page, with elimination from the central compartment.

Basically the equation is:

Equation 26.9.1 Basic Convolution Equation

A general linear pharmacokinetic model with elimination via excretion into urine (ke), metabolism (km) or other processes (kother) is shown below.

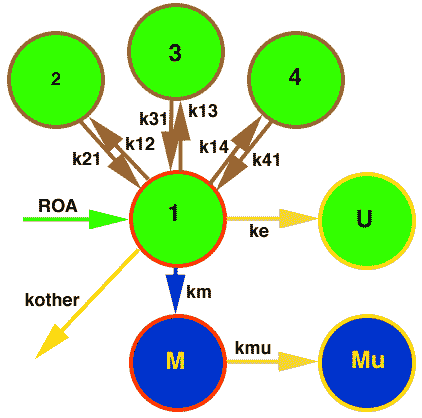
Figure 26.9.1 General Multi Compartment Pharmacokinetic Model

In Figure 26.9.1 the plasma or central compartment is red, the tissue compartments are brown, and the urine component of the model is represented by an orange border. Drug is represented by the filled green circles and metabolite by the blue circle. The overall elimination rate constant, kel, is the sum of all the renal excretion, metabolism and other elimination processes, thus kel = ke + km + kother.

In general the choices we have for the input or route of administration function are:

Route of Administration	Input Function
IV Bolus
IV Infusion - Continuous
IV Infusion¹
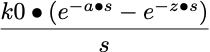
Oral²

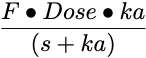
¹ This function includes additional flexibility. 'a' represents the time when the infusion is started and 'z' represents the time when the infusion is stopped. If a = 0 and z = ∞ this simplifies to k0/s.

² The oral dose includes a bioavailability term, F. This is the fraction of the oral dose that is absorbed so F x Dose is the amount of drug which is absorbed into the central compartment.

Functions for more complex absorption processes could be developed.

Disposition functions include:

Number of Compartments	Disposition Function
One
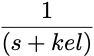
Two¹
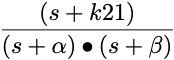
Three²
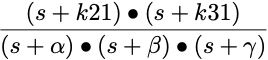
Four³

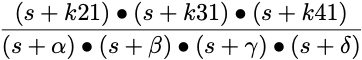
¹ where
α + β = kel + k12 + k21
and
α x β = kel x k21

² where
α + β + γ = kel + k12 + k21 + k13 + k31
α x β + α x γ + β x γ = kel x k21 + kel x k31 + k13 x k21 + k12 x k31 + k21 x k31
and
α x β x γ = kel x k21 x k31

³ where
α + β + γ + δ = kel + k12 + k21 + k13 + k31 + k14 + k41
α x β + α x γ + α x δ + β x γ + β x δ + γ x δ = kel x (k21 + k31 + k41) + k12 x (k31 + k41) + k13 x (k21 + k41) + k14 x (k21 + k31) + k21 x k31 + k21 x k41 + k31 x k41
α x β x γ + α x β x δ + α x γ x δ + β x γ x δ = kel x k21 x k31 + kel x k31 x k41 + kel x k21 x k41 + k12 x k31 x k41 + k13 x k21 x k41 + k14 x k21 x k31 + k21 x k31 x k41
and
α x β x γ x δ = kel x k21 x k31 x k41
with help from de Biasi (de Biasi, J. 1989)

An additional Sample Site multiplier can be appled for other sample sites, beyond drug in the central compartment.

Sample Site functions include:

Sample Site	Function
Drug in Central Compartment
Drug in Peripheral Compartment¹
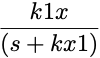
Drug in Urine²
Metabolite in Central Compartment
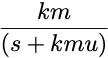
Metabolite in Urine²

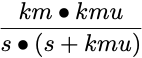
¹ x refers to the 2nd, 3rd, or 4th, peripheral, compartment as shown in Figure 26.9.1.
² Note, drug in urine after an infusion will result in s² in the denominator and an inability to use the finger print method for the back transform step.

Let's try it out:

Select your route of administration, sample, and number of compartments:

Reference

Benet, L.Z. 1972 "General Treatment of Linear Mammillary Models with Elimination from any Compartment as Used in Pharmacokinetics," J. Pharm. Sci., 61:536-541

This page was last modified: Sunday, 28th Jul 2024 at 5:08 pm

Privacy Statement - 25 May 2018

Material on this website should be used for Educational or Self-Study Purposes Only

Pharmacy Math Part One
A selection of Pharmacy Math Problems

IV Bolus		One Compartment
IV Infusion - Continuous		Two Compartment
IV Infusion		Three Compartment
Oral	Drug Amount in the Central Compartment, the Peripheral Compartment (x) or Urine OR Metabolite Amount in the Central Compartment or Urine	Four Compartment