



The equation for Cp versus time is shown above. At the end of the infusion period when t = T the plasma concentration can be calculated as:-
![]()
Equation VI-5. Concentration at the End of an IV Infusion
Once the infusion is stopped all we have is a first order elimination.
Then
![]()
Equation VI-6. Concentration after an IV Infusion has Stopped
where t is time counted from the start of the infusion. Then t - T is the time since the end of the infusion. Then
![]()
Equation VI-7. Concentration during and after an IV Infusion
for t > T
If t is less than or equal to T then set T = t. Then the term e-kel * (t-T) becomes = 1 and is not needed.
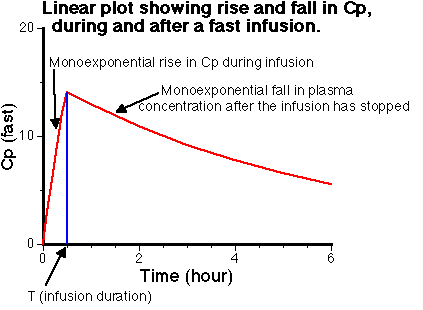
Figure VI-5. Linear Plot of Cp versus Time for Interrupted Infusion. Showing Monoexponential Rise and Fall
That is if we stop the loading infusion and don't start the maintenance infusion.
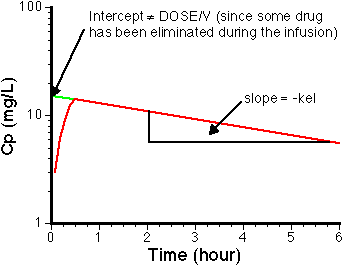
Figure VI-6. Semi-log Plot of Cp versus Time. NOTE: Intercept is not Cp0
![]() = 14.1 x
0.5 = 7.05 mg/L
= 14.1 x
0.5 = 7.05 mg/L
Thus 4 hours after the infusion was stopped the Cp has fallen to half the value at the end of the infusion, remember we started with the drug half-life equal to 4 hours.
| Time (hr) | 3 | 5 | 9 | 12 | 18 | 24 |
| Cp (mg/L) | 12 | 9 | 8 | 5 | 3.9 | 1.7 |
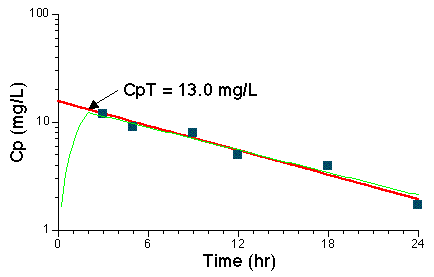
Figure VI-7. Plot of Cp Versus Time after a Two-Hour Infusion
The red line drawn through the data points and back to the Y-axis represents the best-fit line.
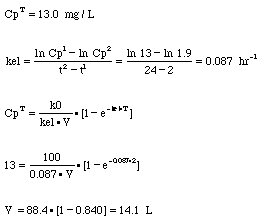
|
Calculate kel and V given post infusion Cp versus time data
|
Copyright 2002 David W.A. Bourne



