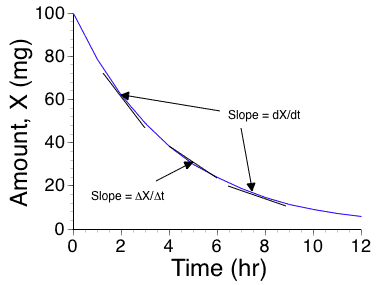
Figure 2.6.1 Linear plot of Amount, X, versus Time
return to the Course index
previous | next
Differential calculus is involved with the study of rates of processes. The calculus part comes in when we look at these processes in detail, that is, during small time intervals.
We may say that at time zero a patient has a concentration of 25 mg/L of a drug in plasma and at time 24 hours the concentration is 5 mg/L. That may be interesting in itself, but it doesn't give us any idea of the concentration between 0 and 24 hours, or after 24 hours. Using differential calculus we are able to develop equations to look at the process during the small time intervals that make up the total time interval of 0 to 24 hours. Then we can calculate concentrations at any time after the dose is given.
In many cases the rate of elimination of a drug can be described as being dependent on or proportional to the amount of drug remaining to be eliminated. That is, the process obeys first order kinetics. This can illustrated by Figure 2.6.1.

Figure 2.6.1 Linear plot of Amount, X, versus Time
This can be described mathematically using Equation 2.6.1.
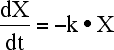
Equation 2.6.1. Rate of Change of X with Time
where k is a proportionality constant we call a rate constant and X is the amount remaining to be eliminated. Note the use of the symbol 'd' to represent a very small increment in X or t. Thus dX/dt represents the slope of the line (or rate of change) over a small region of the curved line, see Figure 2.6.1. When data are collected at discrete times such as 4 and 6 hours the larger change in X and t can be represented by ΔX/Δt as shown in Figure 2.6.1. Note the slope changes as the value of X (y-axis) changes.

Equation 2.6.2. Rate of Elimination
Integration of Equation 2.6.1 (and other differential equations) provides the integrated equations such as Equation 2.6.3.
Equation 2.6.3. Integrated Equation. X versus Time
Equation 2.6.3 is the resulting integrated equation. We will talk more of these equations during the semester.
What we have done is convert the equation for rate of change of X versus time into an equation for X versus time. A differential equation is converted into an integrated equation. (Compare Equation 2.6.1 and Equation 2.6.3).
We will work with both differential and integrated equations in this course.
Another example of integration is the calculation of the area under the plasma concentration versus time curve. Later we shall learn that this summation or integration process can be used to evaluate dosage forms, that is it can be used as a measure of dosage form performance.
In the section above we converted from the rate of change equation to an equation for X. We can also go further and get an area under the curve, which is a further integration.
Another example is the progression from distance, to speed (the rate of change of distance), to acceleration (the rate of change of speed).

Figure 2.6.1 Relationship between Rate and Integral
Material on this website should be used for Educational or Self-Study Purposes Only
Copyright © 2001 - 2026 David W. A. Bourne (david@boomer.org)
 | A game to aid recognizing brand versus generic drug names See how many names you can catch before you run out of lives |
|