 |
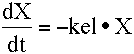 |
| Equation 4.9.1 Rate of Change of Cp versus Cp | Equation 4.9.2 Elimination Rate versus Amount Remaining, X |
return to the Course index
previous | next
The elimination rate constant is the proportionality constant relating the rate of change drug concentration and concentration OR the rate of elimination of the drug and the amount of drug remaining to be eliminated.
 |
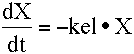 |
| Equation 4.9.1 Rate of Change of Cp versus Cp | Equation 4.9.2 Elimination Rate versus Amount Remaining, X |
By inspection of Equations 4.9.1. or 4.9.2 it can be seen that the units for kel are time-1, for example hr-1, min-1, or day-1. In both equations the rate expression is divided by Cp or X, respectively to provide units for kel. Thus:
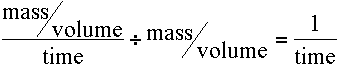 |
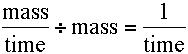 |
| Units for kel from Equation 4.9.1 | Units for kel from Equation 4.9.2 |
From the integrated equation presented on the previous page:
Equation 4.9.3 Ln(Cp) versus time
Plotting ln(Cp) values versus t, time should result in a straight line with a slope equal to -kel, thus kel can be calculated as:

Equation 4.9.4 kel from -slope
Thus with two value for Cp and time data a value for kel can be determined. With more than two Cp - time data points it is possible to plot the data on semi-log graph paper and draw a 'best-fit' line through the data points. This plot is shown on the previous page. The best answer for kel can be calculated by taking points at either end of the 'best-fit' line. This approach has been covered in more detail earlier in Chapter 2.
Equation 4.6.6, presented earlier on the page describing apparent volume of distribution, can be used to calculate concentration at any time, t, after an IV dose with kel and V. Click on Figure 4.8.1 to try this out.

Figure 4.8.1. Concentration versus time
Click on the figure to view the interactive graph
| Drug | kel, hr-1 |
| Acetaminophen | 0.277 |
| Diazepam | 0.021 |
| Digoxin | 0.0161 |
| Gentamicin | 0.347 |
| Lidocaine | 0.39 |
| Theophylline | 0.126 |
Material on this website should be used for Educational or Self-Study Purposes Only
Copyright © 2001 - 2026 David W. A. Bourne (david@boomer.org)
 |
The Book Pharmacokinetics This Course in ePub format |
 |