Boomer Manual and Download
PharmPK Listserv and other PK Resources
Previous Page	Course Index	Next Page

Mathematical Models

As mentioned earlier, pharmacokinetic models are described as equations or formulas. in general there is a dependent variable (y variable) expressed as a function of independent variable(s) (x variable) with various constants and/or parameters.

Figure 6.6.1 The dependent variable is a function of the independent variable(s) and ...

Constants and parameters may be interchangeable or considered very similar. From a modeling point of view parameters are values that are determined by the computer program. Constants are terms that are held fixed during the modeling process.

Mathematical models take many forms. The simplest form is probably the equation for a straight line.

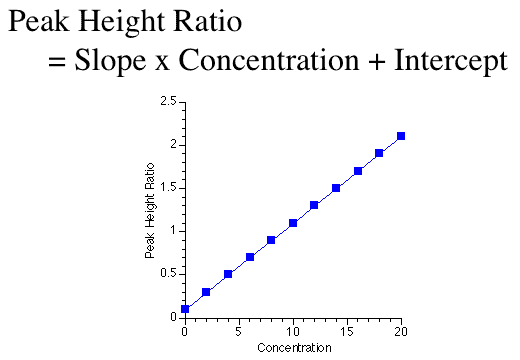
Figure 6.6.2 Linear plot of y versus x for a straight line

In Figure 6.6.2 peak height ratio is the dependent variable and concentration is the independent variable. Slope and intercept are parameters. This is an equation that is very useful for standard curves used in drug analysis.

A pharmacokinetic model is the next example. This is a very simple example which is a not a straight line unless it is transformed. As an exponential equation there was usually two parameters, kel and V, with dose as the constant.

Figure 6.6.3 Linear plot of drug concentration versus time

A third example is a pharmacological equation relating drug effect to drug concentration using a form of the Hill equation. The parameters in this model are E_Max, EC_50% and γ.

Plot of drug effect versus concentration

Figure 6.6.4 Linear plot of drug effect versus drug concentration

return to the Course index

This page was last modified: Sunday, 28th Jul 2024 at 4:46 pm

Privacy Statement - 25 May 2018

iBook and pdf versions of this material and other PK material is available