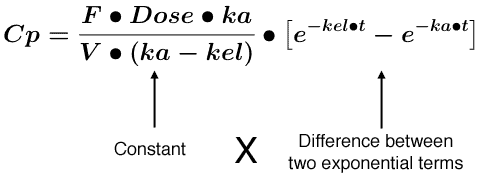
Equation 8.3.1 Drug Concentration after an Oral Dose
return to the Course index
previous | next
If we use F • DOSE for Xg0 where F is the fraction of the dose absorbed, the integrated equation for Cp versus time is shown in Equation 8.3.1.
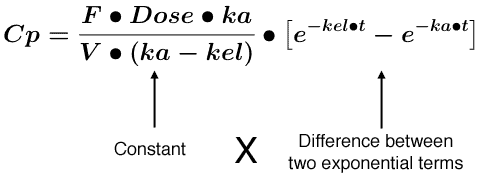
Equation 8.3.1 Drug Concentration after an Oral Dose
Notice that the right hand side of this equation (Equation 8.3.1) is a constant multiplied by the difference of two exponential terms. A biexponential equation.
We can plot Cp as a constant times the difference between two exponential curves (see Figure 2.2.1). If we plot each exponential separately.
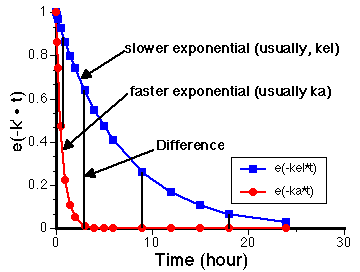
Figure 8.3.1 Linear Plot of e-k' x t versus Time for Two Exponential Terms
Notice that the difference starts at zero, increases, and finally decreases again toward a value of zero.
Plotting this difference multiplied by
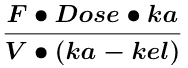 gives Cp versus time.
gives Cp versus time.
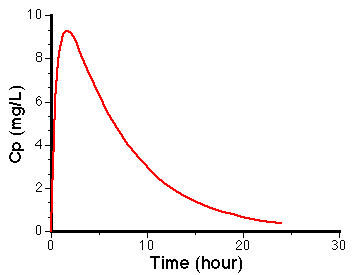
Figure 8.3.2 Linear Plot of Drug Concentration versus Time
We can calculate the plasma concentration at anytime if we know the values of all the parameters of Equation 8.3.1.

The parameters CL, kel and V are dependent on the drug and the patient. Different patients will have different values for CL, kel and V. This might depend on their age, weight, sex, genetic make-up (pharmacogenomics) and/or state of health. Different drugs can have quite different values of CL, kel and V.
While dose is clearly a parameter associated with the dosage form, the parameters F and ka are partly determined by the drug and patient and also by the dosage form or route of administration. The rate (ka) and extent (F) of absorption can depend on the drug and patient with respect to transfer from the site of administration to the blood stream. The value of F may be reduced by poor solubility, drug instability, metabolism by intestinal flora, metabolism or reverse transport by various enzyme systems. The value of ka will be influenced by the drug dissolution rate and ability of the drug to move across any barriers between the site of administration and the blood stream. Both F and ka can also be influenced by the drug dosage form. Generally F is maximize but reduced values of ka may be desired to produce a sustained release effect.
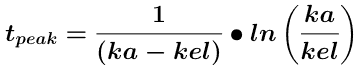
Equation 8.3.2 Time of Peak Concentration after an Oral Dose, tpeak or tmax
As an example we could calculate the peak plasma concentration given that F = 0.9, Dose = 600 mg, ka = 1.0 hr-1, kel = 0.15 hr-1, and V = 30 liter.
Using Equation 8.3.2
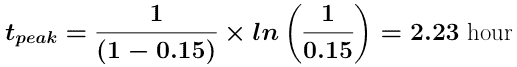
and now using Equation 8.3.1 we can calculate Cppeak or Cpmax for a single oral dose
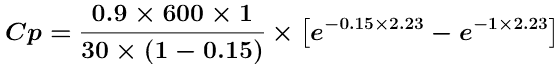
![]()
As another example we could consider what would happen with ka = 0.2 hr-1 instead of 1.0 hr-1
Using Equation 8.3.2
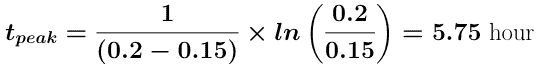
and now using Equation 8.3.1 we can calculate Cppeak or Cpmax for a single oral dose
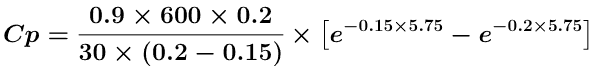
![]()
Note the peak drug concentration is lower and slower with the smaller ka value.
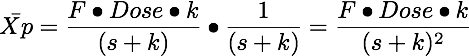
Equation 8.3.3 Laplace of Amount in the Body/Plasma (Xp) where kel = ka = k
Equation 8.3.3 was converted to an equation for amount versus time, Equation 8.3.4, using the Laplace table provided by Mayersohn and Gibaldi (1970).
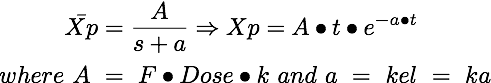
Equation 8.3.4 Amount of drug in plasma, Xp, versus time
Rearranging gives an equation for concentration versus time, Equation 8.3.5.
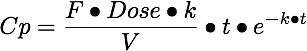
Equation 8.3.5 Concentration of drug, Cp, versus time, where kel = ka
Equation 8.3.5 was used when calculating concentration versus time for simulations when ka = kel. The time of maximum concentration, tpeak, can be calculated with Equation 8.3.6, derived by setting dX/dt = 0 = k • Xg - k • Xp (Equation 8.2.3) and substituting in values for Xg (= F • Dose • e-k • t) and Xp (= F • Dose • k • t • e-k • t).
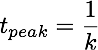
Equation 8.3.6 Time of maximum concentration, tpeak, versus time, where kel = ka
return to the Course index
previous | next
Material on this website should be used for Educational or Self-Study Purposes Only
Copyright © 2001 - 2026 David W. A. Bourne (david@boomer.org)
 |
The Book Pharmacokinetics This Course in ePub format |
 |