Chapter 19 Multi-Compartment Pharmacokinetic Models

return to the Course index
previous | next

Intravenous Administration

Scheme or diagram

Figure 19.2.1 Two Compartment Pharmacokinetic Model

Clearance Model
Equilibrium Model

Differential equation

The differential equation for drug in the central compartment following intravenous bolus administration is:-

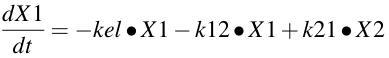
Equation 19.2.1 Differential Equation for the Central Compartment

The kel • X1 term describes elimination of the drug from the central compartment, while the k12 • X1 and k21 • X2 terms describe the distribution of drug between the central and peripheral compartments. Writing differential equations can be reviewed in Chapter 2.

Integrated equation

Integration of this equation (using Laplace transforms) leads to a biexponential equation for plasma concentration as a function of time, Equation 19.2.2

Equation 19.2.2 Integrated Equation for Plasma Concentration versus Time

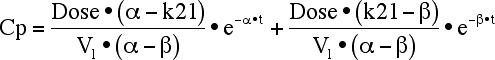
Equation 19.2.3 Integrated Equation for Cp versus Time including k21 and V₁

with α > β and

B =

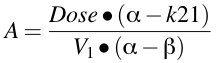
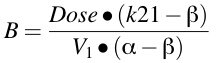
Equation 19.2.4 Calculating values for A and B

The A, B, α, and β terms were derived from the micro-constants during the integration process. They are functions of the micro-constant k12, k21, kel and V1

Using the substitutions for the sum and product of α and β.

α + β = kel + k12 + k21

α • β = kel • k21

If we know the values of kel, k12 and k21 we can calculate α + β as well as α • β. Substituting these values into Equation 19.2.3 gives us values for α and β.

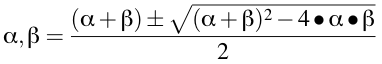
Equation 19.2.5 Converting from kel, k12 & k21 to α & β

Note, in this equation, α is calculated when '+' is used in the numerator and β is calculated when '-' is used in place of the '±'. Thus α is greater than β.

Once we have values for α and β we can calculate values for A and B using Equation 19.2.4.

An example calculation (from the homework)

"A drug follows first order (i.e. linear) two compartment pharmacokinetics. After looking in the literature we find a number of parameter values for this drug. These numbers represent the micro constants for this drug. In order that we can calculate the drug concentration after a single IV bolus dose these parameters need to be converted into values for the macro constants. The kel and V1 for this drug in this patient (90.5 kg) are 0.192 hr^-1 and 0.39 L/kg, respectively. The k12 and k21 values this drug are 1.86 and 1.68 hr^-1, respectively. What is the plasma concentration of this drug 1.5 hours after a 500 mg, IV Bolus dose. In order to complete this calculation first calculate the appropriate A, B, α and β values."

Since α + β = kel + k12 + k21 = 0.192 + 1.86 + 1.68 = 3.732

and

α x β = kel x k21 = 0.192 x 1.68 = 0.32256

Now:

α = [(a+b) + sqrt((a+b)² - 4xaxb)]/2 = [3.732 + sqrt(3.732² - 4x0.32256)]/2 = [3.732 + 3.5549]/2 = 3.643 hr^-1

β = [3.732 - 3.5549]/2 = 0.08853 hr^-1

A = Dose x (α - k21)/[V1 x (α - b)] = 500 x (3.643 - 1.68)/[90.5 x 0.39 x (3.643 - 0.08853)] = 500 x 1.963/[35.295 x 3.55447] = 7.824 mg/L

B = Dose x (k21 - b)/[V1 x (α - b)] = 500 x (1.68 - 0.08853)/[35.295 x 3.55447] = 6.343 mg/L

The last step is

Cp = α x e^{(-α x t)} + β x e^{(-β x t)} = 7.824 x e^{(-3.643 x 1.5)} + 6.343 x e^{(-0.08853 x 1.5)} = 7.824 x 0.004234 + 6.343 x 0.8756 = 0.0331 + 5.5542 = 5.59 mg/L

Later in this chapter we will use equations for the reverse process of converting α, β, A and B into values for k12, k21, kel and V₁.

return to the Course index

This page was last modified: Sunday, 28th Jul 2024 at 5:02 pm

Privacy Statement - 25 May 2018

Material on this website should be used for Educational or Self-Study Purposes Only

Name the Drug
A game to aid recognizing brand versus generic drug names
See how many names you can catch before you run out of lives

Dose:
V₁:
kel:
k21:
k12:

A is:
α is:
B is:
β is: