Chapter 19 Multi-Compartment Pharmacokinetic Models

return to the Course index
previous | next

Parameter Determination

Method of residuals

Values for kel, k12, k12 and other parameters can be determined by first calculating A, B, α, and β. For this we can use the method of residuals (in a similar fashion to determining ka and kel for the one compartment model after oral administration). Starting with the equation for Cp.

Equation 19.3.1 Concentration versus time after an IV Bolus Dose, Two Compartment Model

By definition α is greater than β then as t approaches ∞, e^{-α • t} approaches 0 faster than e^{-β • t}. Therefore if the ratio α/β is large enough (greater than 5) the terminal data points will fall on the line

Equation 19.3.2 Equation for Cp^late versus time

This equation is similar to the equation for the late plasma concentration values after oral administration with a one compartment model. This will be a straight line if plotted on semi-log graph paper.

Figure 19.3.1 Semi-Log Plot of Cp Versus Time Showing Cp^late Extrapolated Back to B

From the slope of this line a value of β can be determined.

Equation 19.3.3 Determining β from the Cp_late Line

The units for β and α, below, are reciprocal time, for example min^-1, hr^-1, etc.

Biological half-life or Terminal half-life

The t_1/2 calculated as 0.693/β is often called the biological half-life or terminal half-life. It is the half-life describing the terminal elimination of the drug from plasma. [For the one compartment model the biological half-life was equal to 0.693/kel].

The difference between the Cp^late values (red line) at early times and the actual data at early times is again termed the 'residual'

Equation 19.3.4 Equation for Residual versus time

Figure 19.3.2 Semi-Log Plot of Cp Versus Time Showing Residual Line and Cp_late Line

Click on the figure to view as an interactive graph

The slope of the residual line (green line) will provide the value of α and A can be estimated as the intercept of the concentration axis (y-axis). A more accurate value for the α value can be determined by expanding the scale on the time axis (Figure 19.3.3). Don't forget to use the new time values when calculating α from the equation

Equation 19.3.5 Determining α from the Residual Line

Figure 19.3.3 Semi-Log Plot of Cp Versus Time Showing Residual Line and Cp Data - NOTE the expansion of the time axis (x axis)

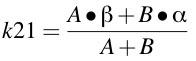
Converting macro constants to micro constants

With A, B, α, and β determined using the method of residuals we can calculate the micro-constants from the equations.

Equation 19.3.6 Converting from A, B, α & β to kel, k12 & k21

Dose:
A:
α:
B:
β:

kel is:
k12 is:
k21 is:
V₁ is: