
Figure 20.4.1 Diagram representing and IV Administration, One Compartment Model with Metabolism
| Boomer Manual and Download | ||||
| PharmPK Listserv and other PK Resources | ||||
| Previous Page | Course Index | Next Page | ||

Figure 20.4.1 Diagram representing and IV Administration, One Compartment Model with Metabolism
Data were simulated for drug and metabolite concentrations are shown in Table 20.4.1
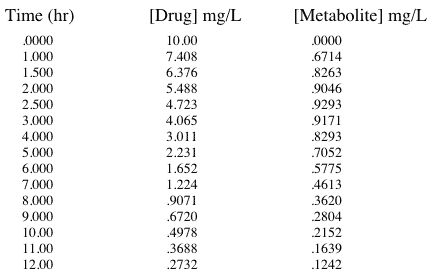
Table 20.4.1 Data Simulated for Cp and Cm
The data were then fitted to the model in Figure 20.4.1 using Boomer.
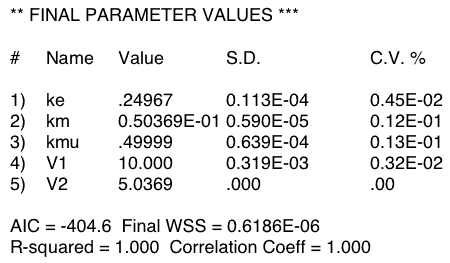
Figure 20.4.1 Output from Boomer
Figure 20.4.1 shows just one result from fitting the data in Table 20.4.1. Note that the CV% values look good for most of the parameters. This generally indicates a good fit and well defined parameters. However, the value of zero for V2 (= Vm) is not a good sign. The real problem becomes apparent when the model is fit multiple times with the same data. Now we see a variety of values for ke, km and Vm. Curiously if the best-fit ke and km values are plotted it can be seen that they fall on a line indicating a common value of kel (= ke + km).
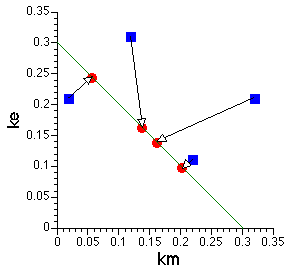
Figure 20.4.2 Plot of ke versus km
The blue squares represent the initial values used for each fit and the red circle represents the final, best-fit, value. Note that all the red circles fall on a straight line representing the value of kel (= ke + km). This indicates the neither ke nor km are identifiable but does suggest that kel is identifiable.

Figure 20.4.3 Output from Boomer - 500 mg Dose

Figure 20.4.4 Output from Boomer - 5 mg Dose
Notice that the CV% for the low dose are quite large (720%) indicating that Vm (=Vmax) and Km are not identifiable with these low dose data. Note also that the parameters have hit reasonable upper limits. Increasing the limits resulted in the values increasing to the new limits. The value for the parameter CV% using the high dose data are much better. The final parameter values for all three estimated parameters are close to the starting values. This indicates that if data as good as the simulated data were available then these parameters would be identifiable.
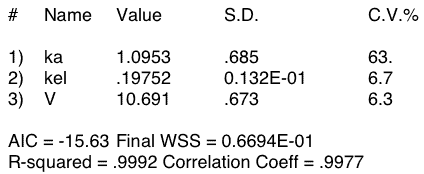
Figure 20.4.5 Output from Boomer - Oral Administration with Missing Early Data Points
Notice the high value for CV% for the ka parameter value compared with the CV% for kel and V. Clearly ka is not well defined.
SUBROUTINE SETMOD
INTEGER K,P
CHARACTER MDNM*10
COMMON /MOD/ K,P
COMMON /MODN/ MDNM
K = 4
P = 3
MDNM = 'Model 3'
RETURN
END
|
K = Number of compartments (diff eqns)
P = Number of model parameters (rate constants) Volumes (intensity parameters) are entered as experimental parameters during execution |
SUBROUTINE DERIVS(X,Y,DYDX,THETA)
PARAMETER (NMAX=25)
REAL*8 X,Y(NMAX),DYDX(NMAX),THETA(35)
dydx(1) = -(theta(1) + theta(2)) * y(1)
dydx(2) = theta(1) * y(1)
dydx(3) = theta(2) * y(1) - theta(3) * y(3)
dydx(4) = theta(3) * y(3)
RETURN
END
|
theta(1) = ke
theta(2) = km theta(3) = kmu
y(i) = amount in compartment i
|
Figure 20.4.6 FORTRAN code Defining the Drug and Metabolite Model
The drug and metabolite model has four components so the model is defined in Figure 20.4.6 using four differential equations. These subroutines are compiled and linked with the main program files to produce a model specific program file.
IDENTIFIABILITY FOR COMPARTMENTAL MODELS COPYRIGHT 1988, THE UNIVERSITY OF MICHIGAN SELECT APPROPRIATE MENU ITEM : 1. NEW EXPERIMENT 2. REVIEW/EDIT EXPERIMENT 3. EXIT MAKE SELECTION (1,2 OR 3) > 1 ENTER NAME FOR EXPERIMENT (UP TO 10 CHARS) > model3 ENTER INITIAL VALUE FOR STATE VARIABLE 1 > 100 ENTER INITIAL VALUE FOR STATE VARIABLE 2 > 0 ENTER INITIAL VALUE FOR STATE VARIABLE 3 > 0 ENTER INITIAL VALUE FOR STATE VARIABLE 4 > 0 |
Enter the name for this experiment and the initial values for each of the compartments. In this case 100 (mg) are added to compartment 1 (IV Bolus) |
ENTER VALUE FOR PARAMETER 1 > .1 ENTER VALUE FOR PARAMETER 2 > .2 ENTER VALUE FOR PARAMETER 3 > 1.5 ENTER TIME INTERVAL > 1 ENTER NUMBER OF TIME POINTS > 9 DO YOU WISH THE PARTIALS PRINTED (Y OR N) ? y DO YOU WISH THE STATE VARIABLES PRINTED (Y OR N) ? y |
Enter values for the model parameters, ke, km and kmu
This version use equaling spaced time values, enter the time interval and the number of data points |
ENTER THE NUMBER OF ROWS IN THE C-MATRIX > 1 ENTER C-MATRIX IN ROW ORDER. ROW 1 > 1,1,1,1 ENTER THE NUMBER OF EXPERIMENTAL PARAMETERS > 2 ENTER VALUE FOR EXPERIMENTAL PARAMETER 1 > 10 ENTER VALUE FOR EXPERIMENTAL PARAMETER 2 > 15 NUMBER OF TIMES PARAMETER 1 APPEARS IN THE C-MATRIX > 1 ENTER C-MATRIX POSITION (I,J) FOR EXPERIMENTAL PARAMETER 1 OCCURENCE 1 > 1,1 NUMBER OF TIMES PARAMETER 2 APPEARS IN THE C-MATRIX > 1 ENTER C-MATRIX POSITION (I,J) FOR EXPERIMENTAL PARAMETER 2 OCCURENCE 1 > 1,3 DO YOU WISH TO MAKE ANY CHANGES TO THE ABOVE EXPERIMENT (Y OR N) ? n CONTINUE WITH EXPERIMENT model3 ? y |
This is where it gets a little tricky (corrections and comments welcome)
The C-matrix defines the observation layer. There is usually only one row, unless, for example, you have concentration and (linear) response from the same compartment. Enter '1' for each compartment. The two experimental parameters are V and Vm. Enter experimental parameter values (here expressed as volumes but may need to be reciprocal volume), each appearing once in the C-matrix. V is in row 1, column 1 (i.e. compartment one) and Vm is in row 1, column 3 (i.e. compartment three). Entering these parameters associated columns 1 and 3 indicates that Cp and Cm are measured in this experiment |
ENTER NAME FOR OUTPUT FILE (UP TO 10 CHARACTERS)
> ident23
CALCULATING VALUES FOR STATE VARIABLES.....
OBTAINING PARTIALS MATRIX.....
CALCULATING G'G MATRIX.....
PERFORMING ROW REDUCTION.....
NON-IDENTIFIABLE PARAMETERS :
1 2 5
IDENTIFIABLE PARAMETERS :
3 4
DO YOU WISH THE CORRELATION MATRIX ( 2x 2)
PRINTED TO THE SCREEN (Y OR N)? y
CORRELATION MATRIX
3 4
3 1.00 0.92
4 0.92 1.00
SELECT APPROPRIATE MENU ITEM :
1. NEW EXPERIMENT
2. REVIEW/EDIT EXPERIMENT
3. EXIT
MAKE SELECTION (1,2 OR 3) > 3
|
The result: Parameters 1 (ke), 2 (km) and 5 (Vm) are non-identifiable
and parameters 3 (kmu) and 4 (V) are identifiable |
iBook and pdf versions of this material and other PK material is available
Copyright © 2001-2022 David W. A. Bourne (david@boomer.org)