Chapter 22 Pharmacodynamic Models

return to the Course index
previous | next

Concentration Effect Relationships

The basic premise for the clinical utility of pharmacokinetics is that there is a clearly defined relationship between drug concentration in readily available samples and drug response. Application of pharmacokinetic methods allows us to account for the variability in an individual's ability to absorb, distribute, metabolize and excrete drugs. The objective of these methods is to control the drug concentration in blood or plasma and potentially other fluids and tissues. For this approach to be effective there needs to be a relationship between these concentrations and the response to the drug. In some cases the response is direct and reversible and the Hill equation or some variation of it may be be applied. In other cases the reversible response may be indirect, often with a sequence of events required. It is also possible that a drug will produce an irreversible response.

Direct Reversible Effects

Examples of direct reversible effects might include blood pressure control or muscle relaxation. For many drugs the response is directly related to the drug concentration at the receptor site which in turn is related to the concentration in plasma. As the receptor concentration increases so does the response and with lower concentration the response drops.

Figure 22.2.1 Direct Reversible Response

In general the receptor might be 'mathematically' within the central compartment, a peripheral compartment or a separate effect compartment. In each case the relationship between concentration at the receptor and the response might be described with a Sigmoid E_max model (Hill equation)

Equation 22.2.1 Sigmoid E_max Response versus Concentration, C_R (Hill Equation)

Equation 22.2.2 Sigmoid E_max Response versus Concentration, C_R (Hill Equation) with Baseline Response

In Equations 22.2.1 and 22.2.2, E_max is the maximum response, C_{R, 50%} is the concentration which produces a 50% maximum response (often called EC_50%) and γ is a slope factor. For responses which increase from zero, Equation 22.2.1 is more appropriate. In other cases where the response is an increase or decrease from a baseline value Equation 22.2.2 may be a better choice. Another version of this equation, Equation 22.2.1, is the E_max model but this is just the same except that γ is set to 1.

Equation 22.2.1 can be illustrated in Figure 22.2.2 as a sigmoid curve.

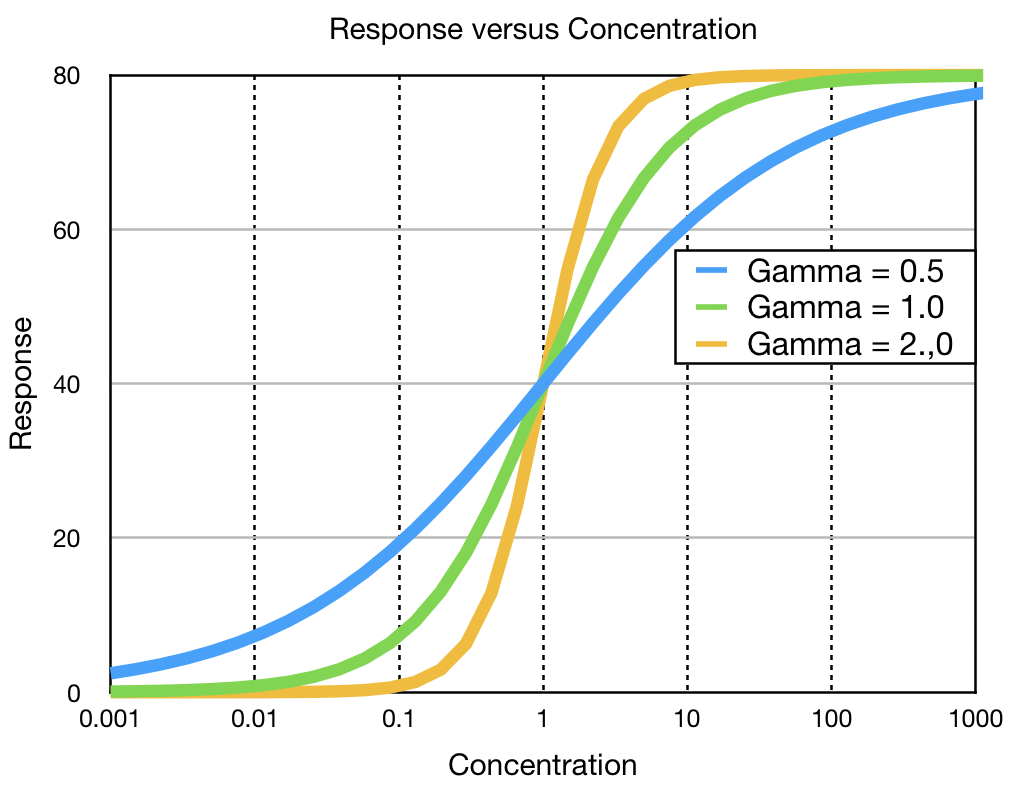
Figure 22.2.2 Response versus Concentration (Log scale)

where E_max is 80, C_{R, 50%} is 1 and gamma is 0.5, 1 or 2.

With data such as response versus concentration we could readily fit the data with a Hill equation model using Boomer, SAAM II or some other non-linear regression program. We could also add appropriate weight to the data and include a second response to a fitted model.

Another approach is to rearrange the Hill equation to produce a Logarithmic model, Equation 22.2.3.

Equation 22.2.3 Linear version of the Hill equation

Plotting log[Response/(E_max - Response)] versus log(C_R) should produce a straight line graph with a slope of γ and intercept of -log C^γ_{R, 50%}.

Another more commonly used Logarithmic model can be derived empirically from the Hill equation if we look at the response versus log concentration plot between 20 to 80% maximum response. Notice the straight line portion.

Figure 22.2.3 Plot of Response versus Concentration with log-linear portion

This region of the full response concentration curve can be described by Equation 22.2.4.

Equation 22.2.4 Logarithmic model for the middle part of the curve

This might be useful if the concentration isn't high enough to estimate E_max. It is also interesting to consider concentrations after an IV bolus, one compartment model in this log form, equating plasma concentration and receptor concentration assuming the receptor is close to the plasma or central compartment.

Equation 22.2.5 log(C) versus time

and

Equation 22.2.6 Response versus time

Note that with this scenario the response decreases linearly with time. One example of this is the results after the last dose of a one week regimen of labetalol (Derendorf and Hochhaus 1995).

With each of these variations we see a direct, immediate relationship between response and concentration. The higher the concentration the higher the response. Note, the receptor may be within the central compartment or a peripheral compartment. It might be in a region where there is little drug amount and thus doesn't show up as a distinct 'pharmacokinetic' compartment. For this situation we might need to include a 'small' effect compartment. We can explore this by looking at the relationship between response and concentration in various compartments.

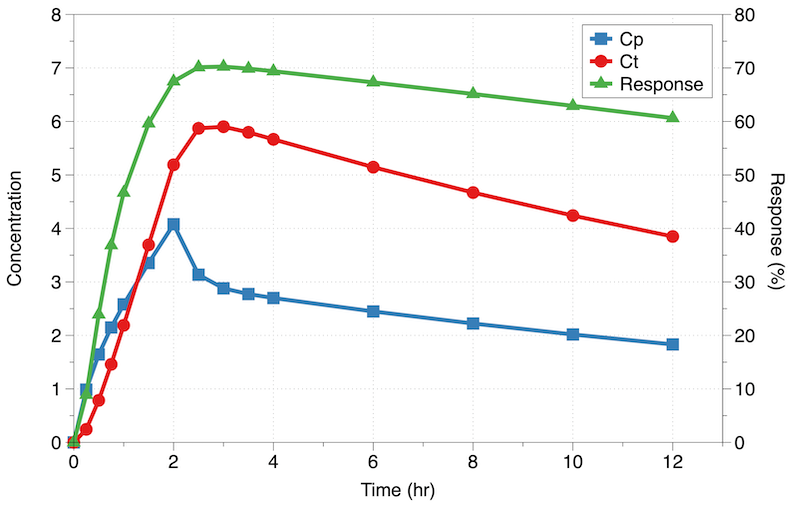
Figure 22.2.4 Plot of Cp, Ct and Response versus Time

One way to explore this aspect of the model, that is, where is the receptor, is to plot response versus concentration. In Figure 22.2.5 we plot response versus the concentration in the central compartment.

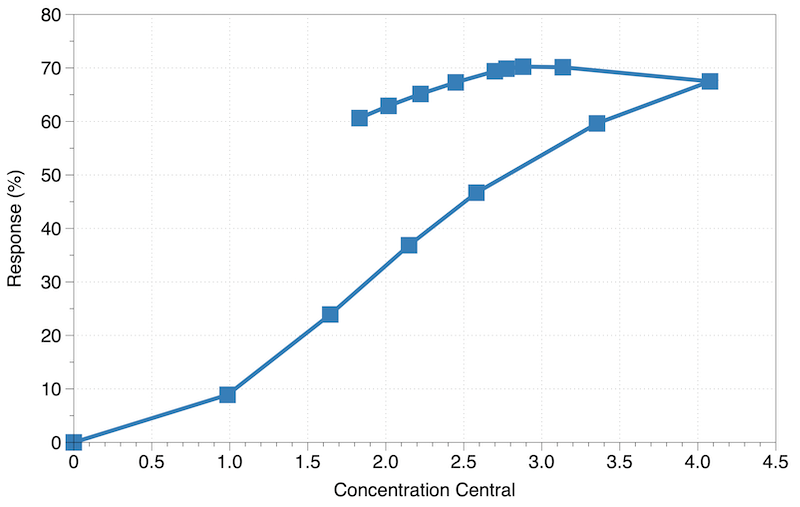
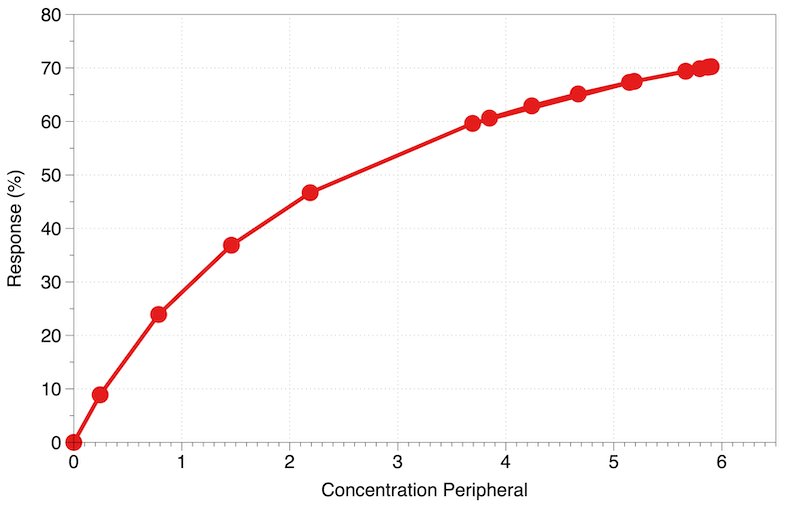
Figure 22.2.5 Response versus Concentration in the Central or Peripheral compartment

In the left panel there is a significant difference in response between the increasing concentration and decreasing concentration (a counterclockwise hysteresis curve) we might assume that the receptor is not in the central compartment. The same plot for the concentration in the tissue or peripheral concentration is shown on the right panel. Note the increasing and decreasing concentration data overlap indicating the receptor for this response is in the peripheral compartment. Wagner et al. (1968) found the response to LSD could be correlated with peripheral drug concentration. A response to digoxin was also correlated with peripheral drug concentrations (Reuning, 1973).

In other case there may not be a correlation between central or peripheral concentrations. For these drugs we might include a hypothetical effect compartment as shown in Figure 22.2.6 (Sheiner et al., 1979).

Figure 22.2.6 Pharmacokinetic Model with Effect Compartment

Want to explore this type of model!

Indirect Reversible Response

The bodies response to anticoagulants or anti-diabetic medication might result from a cascade of processes and thus be considered indirect but reversible. One example is the pharmacodynamics of warfarin described by Nagashima et al. (1969). Although peak concentrations of warfarin occur after a few hours the maximum response to this drug can take a few days. The model used to describe this included degradation and synthesis of prothrombin complex activity.

Irreversible Response

The response from antibiotics and anti-cancer drugs may be considered irreversible responses but the details are often more complex (Jusko 1971). An example is the irreversible effect of aspirin on platelet aggregation which last the life of the affect platelets (7-10 day life span, Lalonde, 2006).

References

Lalonde, R.L. "Pharmacodynamics" Chapter 5 in Applied Pharmacokinetics and Pharmacodynamics: Principle of Therapeutic Drug Monitoring, 4th ed., ed. Burton, M.E., Shaw, L.M., Schentag, J.J. and Evan,s W.E., LWW, Baltimore, MD, 2006
Hill, A. V. 1910 The possible effects of the aggregation of the molecules of hemoglobin on its dissociation curves. J. Physiol. (Lond.), 40, iv-vii.
Hill Equation, Wikipedia entry
Derendorf, H. and Hochhaus, G. Handbook of Pharmacokinetic/Pharmacodynamic Correlation, CRC Press, 1995 page 207
Sheiner, L.B., et al. 1979. Simultaneous modeling of pharmacokinetics and Pharmacodynamics: application to d-tubocurarine, Clin. Pharmacol. Therap., 25, 358-371
Reuning, R.H. et al. 1973 Role of pharmacokinetics in drug dosage adjustment I Pharmacologic effect kinetics and apparent volume of distribution of digixon, J. Clin. Pharmacol., 13, 127-41
Wagner, J.G. et al. 1968 Correlation of performance test scores with "tissue concentrations" of lysergic acid diethylamide in human subjects, Clin Pharmacol. Therap., 9, 635-8
Nagashima, R., O'Reilly, R.A., Levy, G. 1969 Kinetics of pharmacologic response in man: the anti-coagulant action of warfarin, Clin. Pharmacol. Therap., 10, 22-35
Jusko, W.J. 1971 Pharmacodynamics of chemotherapeutic effect: dose-time-response relationships for phase-specific agents, J. Pharm. Sci., 60, 892-5

return to the Course index

This page was last modified: Sunday, 28th Jul 2024 at 5:06 pm

Privacy Statement - 25 May 2018

Material on this website should be used for Educational or Self-Study Purposes Only

Pharmacy Tutorials
A tvOS app which presents
a collection of video tutorials related to
Basic Pharmacokinetics and
Pharmacy Math