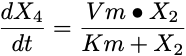Chapter 26
Integrating Differential Equations using Laplace Transforms
return to the Course index
previous | next
Integrating Differential Equations using Laplace Transforms
Student Objectives for this Chapter
- Write differential equation for components of a pharmacokinetic model
- To use the steps involved in integrating differential equations using Laplace Transforms
Writing Differential Equations
Rate processes in the field of pharmacokinetics are usually limited to first order, zero order and occasionally Michaelis-Menten kinetics. Linear pharmacokinetic systems consist of first order disposition processes and bolus doses, first order or zero order absorption rate processes. These rate processes can be described mathematically.
First Order Equation

Each first order rate process ("arrow") is described by a first order rate constant (k1) and the amount or concentration remaining to be transferred (X1).
Zero Order Equation

Zero order rate processes are described by the rate constant alone. Amount or concentration to the zero power is 1.
Michaelis Menten Equation

The Michaelis Menten process is somewhat more complicated with a maximum rate (velocity, Vm) and a Michaelis constant (Km) and the amount or concentration remaining.
The full differential equation for any component of a pharmacokinetic model can be constructed by adding an equation segment for each arrow in the pharmacokinetic model. The rules for each segment:
- Direction of the arrow
- If the arrow goes into the component the equation segment is positive
- If the arrow leaves the component the equation segment is negative.
- Type of rate process
- If the rate process is first order multiply the (first order) rate constant by the amount or concentration of drug in the component at the tail of the arrow.
- If the process is zero order just enter the rate constant.
- For a Michaelis Menten processes include the amount or concentration of drug in the component at the tail of the arrow in the Michaelis-Menten equation.
An example

Figure 2.7.1 An example pharmacokinetic model with zero order, first order and Michaelis Menten processes.
In Figure 2.7.1 the rate process from one to two is zero order. The process from two to three is first order and the process from two to four follows Michaelis-Menten kinetics. We can now systematically write the differential equations for each component of the model.
- Component 1 There is one arrow leading out of component one so the rate process if negative. This process is zero order so we just write the rate constant. The equation for this component is:

- Component 2 This component is more of a challenge. There are three arrows connected with this component. One arrow leads to the compartment so this equation segment is positive. The other two arrows lead away from the component and these equation segments are negative. Starting with the zero order process provides is a positive k0 to the differential equation. The first order process is developed as the rate constant multiplied by the amount remaining in component 2. This is negative and is -k1 x X2. The final segment is the Michaelis Menten process from component 2 to component 4. This is also negative and is described as -Vm x X2/(Km + X2). The total differential equation for this component is:

- Component 3 OK; downhill from here. Now we have one arrow going to this component from component 2, thus the equation segment is positive. The rate process is first order so we multiply the rate constant by the amount remaining in the component at the tail of the arrow, component 2. The equation is:

- Component 4 The fourth component is also described with one equation segment. The arrow leads to this component so the segment is positive. The rate process is a Michaelis Menten process. The equation for this component is:
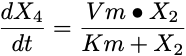
More examples of pharmacokinetic models and writing differential equations and even more examples (Ignore the Laplace parts for now).
This page was last modified: Sunday, 28th Jul 2024 at 5:08 pm
Privacy Statement - 25 May 2018
Material on this website should be used for Educational or Self-Study Purposes Only
Copyright © 2001 - 2025 David W. A. Bourne (david@boomer.org)
 | Name the Drug
A game to aid recognizing brand versus generic drug names
See how many names you can catch before you run out of lives |

|