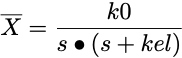
Equation 26.6.1 Laplace Transform of Amount in the Body during an IV Infusion
return to the Course index
previous | next
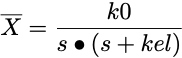
Equation 26.6.1 Laplace Transform of Amount in the Body during an IV Infusion
Note that the denominator has a power of 2 in s and no repeating terms. The numerator has a power of 0 in s. Therefore the fingerprint method can be applied.
Setting the denominator to zero:
s * (s + kel) = 0
gives the two roots 0 and -kel.
The finger print method can then be applied as illustrated in the QuickTime® movie below.
Figure 26.6.1 Movie illustrating the Finger Print Method - 2
The solution
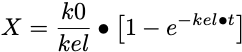
Equation 26.6.2 Integrated Equation for Amount in the Body an IV Infusion
Material on this website should be used for Educational or Self-Study Purposes Only
Copyright © 2001 - 2025 David W. A. Bourne (david@boomer.org)
 | A game to aid in interpreting Prescription Sig instructions See how many Sigs you can catch before you run out of lives |
|