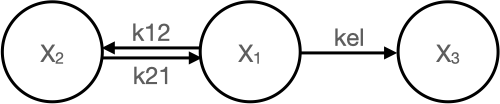
Figure 26.7.1 A Two Compartment Pharmacokinetic Model
return to the Course index
previous | next

Figure 26.7.1 A Two Compartment Pharmacokinetic Model
Following an IV bolus dose the drug is placed in component 1. Drug concentration in this component achieves equilibrium quickly. More slowly the drug either distributes into and out of various tissues and body fluids designated component 2 or is eliminated from the body as described by the first order rate constant, kel. The distribution processes are usually described using first order rate constants. Alternately, the elimination and distribution could be describe by clearance terms. For the purposes of this derivation we will confine the mathematical model to use rate constants. The differential equations for both components are shown below:
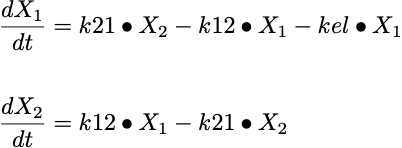
Equations 26.7.1 Differential Equations for the Two Compartment Model after an IV Bolus Dose
Using the rules on a previous page it is possible to write the Laplace transform of each of the equations.
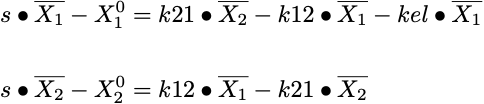
Equations 26.7.2 Laplace Transforms for the Equations 26.7.1
Since the amount of drug in component 2 is zero at time 0 the term, X02 can be set to 0. Equation 26.7.2.b becomes:
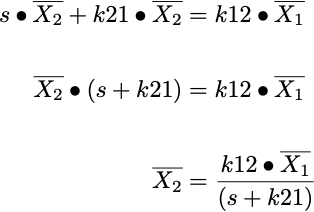
Equation 26.7.3 Laplace Transform of the Amount in Component 2
With X01 the Dose we can substitute the value in Equation 26.7.3 for the Laplace of the amount in component 2 into Equation 26.7.2.b to continue the derivation of the Laplace of component 1.
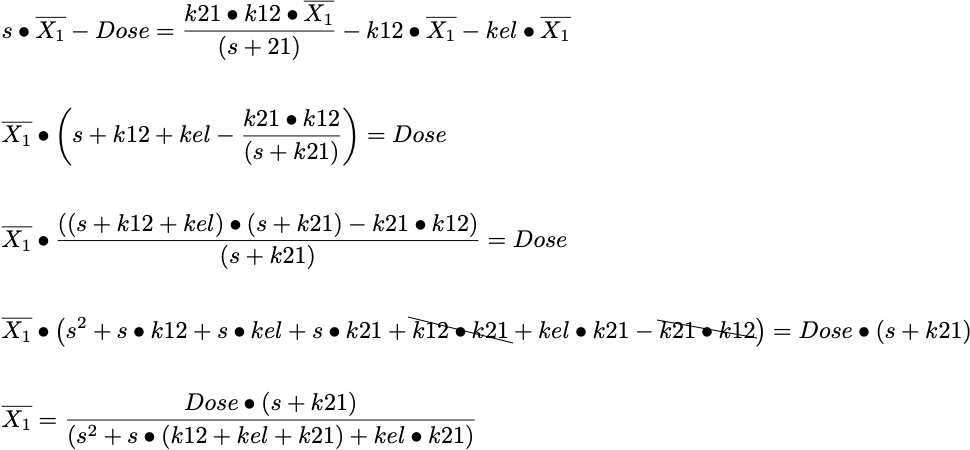
Equation 26.7.4 Deriving the Laplace of the Amount in Component 1
And now the fun stuff. We can make a substitution to simplify Equation 26.7.4. Looking at:
Equation 26.7.5 Introducing the terms α and β
Looking at Equation 26.7.5 and the last term in Equation 26.7.4 we can make the substitutions:
and α x β = kel x k21
to derive the final equation for the Laplace of the amount in component 1.
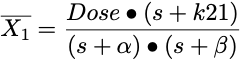
Equation 26.7.6 Laplace of the Amount in Component 1
Reference
Material on this website should be used for Educational or Self-Study Purposes Only
Copyright © 2001 - 2025 David W. A. Bourne (david@boomer.org)
 |
The Book Pharmacokinetics This Course in ePub format |
 |