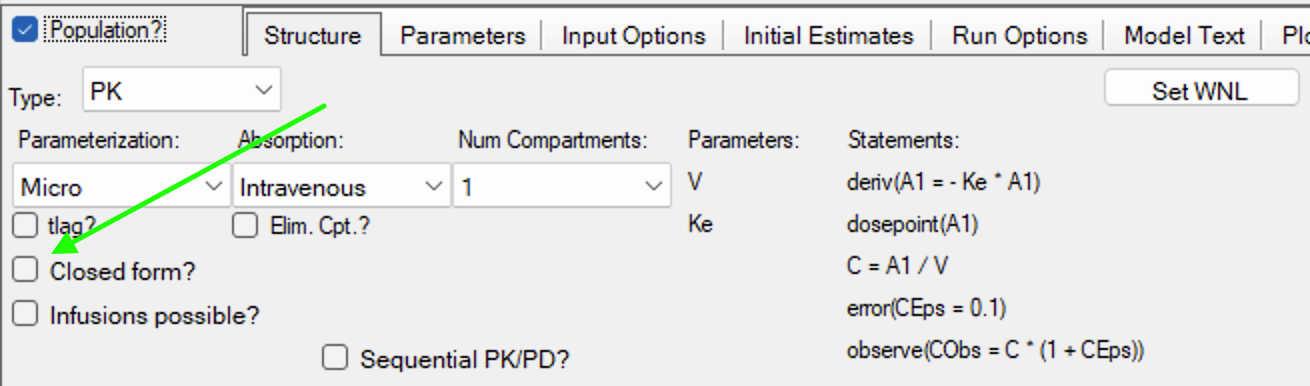
Figure 27.5.1 Uncheck Closed Form for DE Options
return to the Course index
previous | next
| Runge-Kutta | RKF45 | Adam's | Gear's | |
|---|---|---|---|---|
| ka/kel = 1.0 | 15 | 2 | 2 | 2 |
| ka/kel = 10 | 38 | 2 | 3 | 4 |
| ka/kel = 100 | 174 | 7 | 14 | 4 |
| ka/kel = 1000 | * | 50 | 110 | 4 |
The results in Table 27.5.1 were determined using Boomer some time ago when computers were much slower. All the methods except Gear's method slow considerably or fail(*) when the stiffness ratio gets above 100.
Example Boomer .BAT files (and the resulting .OUT files) demonstrating a simulation of a multi-compartment version of the model shown in Table 27.4.1 can be downloaded (Macintosh and Windows). The Runge-Kutta version (rk1.BAT) fails with too many steps when ka > 50. The Runge-Kutta-Fehlberg version (rkf100.BAT) starts to show problems with error messages when ka > 500. Gear's method (gear100.BAT) works with ka = 1.0 x 1012.
Method of Numerical Integration 0) Classical 4th order Runge-Kutta 1) Runge-Kutta-Gill 2) Fehlberg RKF45 3) Adams Predictor-Corrector with DIFSUB 4) Gears method for stiff equations with PEDERV 5) Gears method without PEDERV Enter choice (0-5)
For ordinary compartmental problems choice 2 (Fehlberg RKF45) should be chosen as the most efficient. With stiff systems choice 5 (Gears method without PEDERV) is best.
Each of these numerical integration methods requires that the user specify an upper limit of the acceptable error, either as a relative or as an absolute error. In the case of the Fehlberg RKF45 method both types of error are requested.
Enter Relative error term for
Numerical integration (0.0001)
Enter Absolute error term for
Numerical integration (0.0001)
For each of the other methods only one error term is required (relative for Classical 4th order Runge-Kutta and the Runge-Kutta-Gill method and absolute for Adams Predictor-Corrector or Gears method). This can be important when editing a Boomer .BAT file. An additional line may need to be added if switching to the Fehlberg RKF45 method or a line may need to removed if switching from the Fehlberg RKF45 method.
A final point may need to be made regarding the specification of the absolute error term. At times the default value of 0.001 may be too small. Note that even though the concentration calculated may be quite small, for example, 1 - 10 mg/L the number calculated, internally, may be somewhat higher. For example, with a dose expressed as 1000 mg an absolute error of 0.0001 would mean a change in the 7th significant figure. This may stress the method and thus a larger absolute value may be more appropriate and necessary. The important thing is to consider how realistic the error value might be for the problem being studied.
** ERROR ** ISTEP = 20000
*** Fatal error in RK ***
restart option not selected
Try another integration method
PAUSE Press RETURN to quit statement executed
As indicated in the error message another integration method may be better.
The Runge-Kutta-Fehlberg may be quite efficient for compartmental pharmacokinetic models. However, with stiff systems the program will become inefficient and the error message below will indicate this problem.
IFLAG NOT EQUAL TO 2 4 Number of differential equations 20 Value for line 1 -.2850E-04 X value at beginning of interval 1.764 X value at end of interval 2.000 Relative error .1000E-03 Absolute error .1000E-03
Adjustments to the requested error might help or alternately Gear's method may be used to complete the analysis.

Figure 27.5.1 Uncheck Closed Form for DE Options
The Advanced Run Options tabs provides the ability to adjust the values of relative tolerance (RTOL), the absolute tolerance (ATOL) and the Maximum number of steps (MAXSTEP).
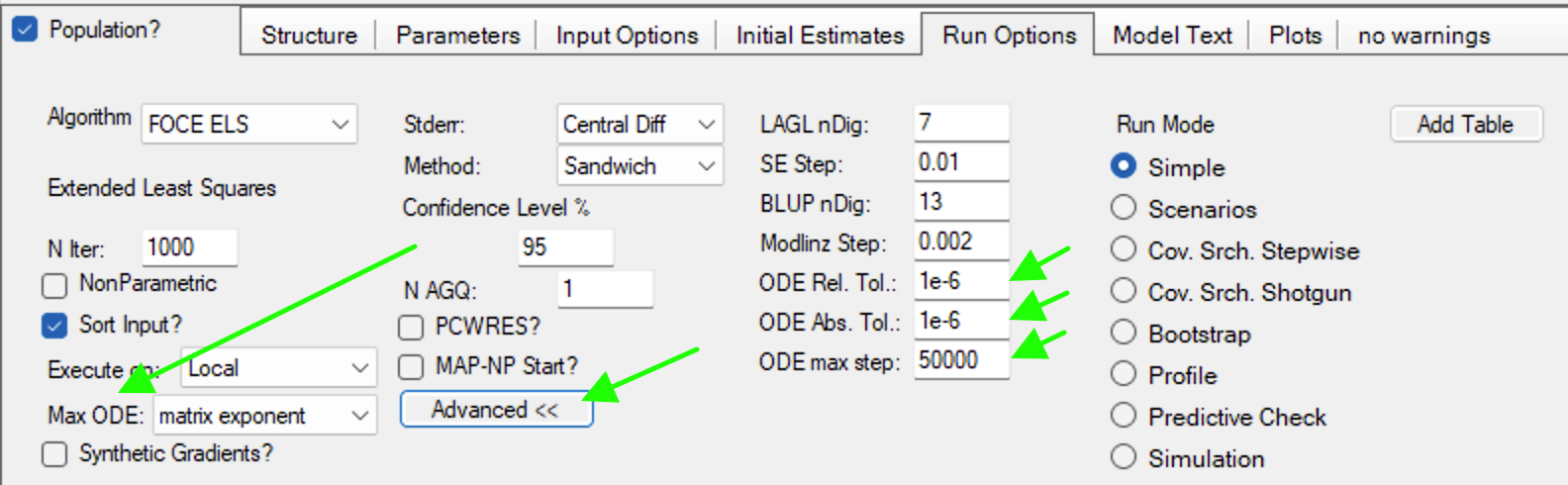
Figure 27.5.2 Select Max ODE method and Advanced for other Options
The Matrix Exponent method is the default, when applicable, and is a very efficient method for ordinary pharmacokinetically relevant systems of differential equations. The LSODE method is similar to Gear's method and is most appropriate with stiff systems. The LSODA method switches between the non-stiff Adam's method and a stiff system method similar to Gear's method. Two non-stiff methods are available. The DVERK method is a Runge-Kutta method based on Verner's 5-6 method and the DPRRI5 method is another Runge-Kutta method of order 4-5.
Material on this website should be used for Educational or Self-Study Purposes Only
Copyright © 2001 - 2025 David W. A. Bourne (david@boomer.org)
 | Pharmacy Math Part Two A selection of Pharmacy Math Problems |
 |