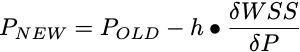
Equation 28.4.1 New parameter value Calculated from WSS Surface
return to the Course index
previous | next
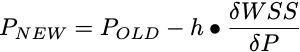
Equation 28.4.1 New parameter value Calculated from WSS Surface
The computer program can estimate the rate of change of WSS with respect to each parameters (δWSS/δP) by making a small change in each parameter and determining the new WSS. This gives a direction. A linear search in this direction provides the value of h for the lowest WSS. This point becomes the old value and a new search is undertaken. With each iteration the program moves closer to the minimum value of the WSS.
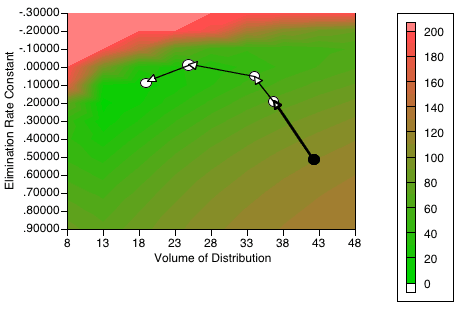
Figure 28.4.1 Contour map of kel versus V showing probable Path of Steepest Descent Method
Advantages of this method
Disadvantages of this method
The steepest descent method is not commonly used on its own to perform a nonlinear least squares best-fit but it does form the basis of another more useful method, Marquardt's method. The linear search, zigzaging down valleys and being so slow near the minimum mean that other methods are more efficient.
Material on this website should be used for Educational or Self-Study Purposes Only
Copyright © 2001 - 2026 David W. A. Bourne (david@boomer.org)
 | Pharmacy Math Part One A selection of Pharmacy Math Problems |
 |