




Advantages: i) The absorption and elimination processes can be quite similar and still accurate determinations of ka can be made.
ii) The absorption process doesn't have to be first order. This method can be used to investigate the absorption process. I have used this type of method to investigate data obtained after IM administration and found that two absorption steps maybe appropriate. Possibly a fast step from drug in solution and a slower step from drug precipitated at the injection site.
Disadvantages: i) The major disadvantage of this method is that you need to know the elimination rate constant, from data collected following intravenous administration.
Theory: The working equations can be derived from the mass balance equation:-
Amount Absorbed (A) = Amount in Body (X) + Amount Eliminated (U)
or A = X + U
Differentiating each term with respect to time gives:-
![]()
or
![]()
or
dA = V * dCp + kel * V * Cp * dt
and integrating gives:-

or

Taking this to infinity, Cp = 0 and
![]()
Finally (Amax - A) is the amount remaining to be absorbed, Xg thus:-
![]()
We can use this equation to look at the absorption process. If absorption is first order
![]()
or
![]()
Thus a plot of ln (Amax - A) versus time will give a straight line for first order absorption with a slope = -ka
Table IX-2 Example Data for the Method of Wagner-Nelson
kel (from IV data) = 0.2 hr-1
| Time (hr) | Plasma Concentration (mg/L) | Column 3 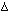 AUC AUC | Column 4 AUC | Column 5 kel * AUC | A/V [Col2 + Col5] | (Amax - A)/V |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 4.9 |
| 1.0 | 1.2 | 0.6 | 0.6 | 0.12 | 1.32 | 3.58 |
| 2.0 | 1.8 | 1.5 | 2.1 | 0.42 | 2.22 | 2.68 |
| 3.0 | 2.1 | 1.95 | 4.05 | 0.81 | 2.91 | 1.99 |
| 4.0 | 2.2 | 2.15 | 6.2 | 1.24 | 3.44 | 1.46 |
| 5.0 | 2.2 | 2.2 | 8.4 | 1.68 | 3.88 | 1.02 |
| 6.0 | 2.0 | 2.1 | 10.5 | 2.1 | 4.1 | 0.8 |
| 8.0 | 1.7 | 3.7 | 14.2 | 2.84 | 4.54 | 0.36 |
| 10.0 | 1.3 | 3.0 | 17.2 | 3.44 | 4.74 | 0.16 |
| 12.0 | 1.0 | 2.3 | 19.5 | 3.9 | 4.9 | - |
 | 0.0 | 5.0 | 24.5 | 4.9 | 4.9 | - |

Figure IX-5, Semi-Log Plot of (Amax-A)/V versus Time

Figure IX-6, Linear Plot of (Amax - A)/V versus Time
Copyright 2001 David W.A. Bourne




