PHAR 4634 - Chapter 9 Page 4

Calculation of F

So far we have looked at the equation for calculating Cp as a function of time, and then methods of determining ka and kel. That is the method of residuals and the Wagner-Nelson method. Now to continue, we can look at methods of calculating F, the extent of absorption, i.e. the fraction of the dose which is absorbed.

Returning to the equation for Cp as a function of time

Equation IX-1 from earlier

we can calculate ka and kel given Cp versus time data. From the method of residuals, the intercept can be determined as

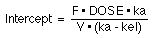
Since we know the DOSE and have calculated ka and kel, it is possible to calculate . However, with only data from a single administration available that's all we can determine, we cannot separate V and F. Of course if we have IV data for kel and V, we could use this to determine F.

Thus F must be determined by comparison with another dose administration. If the other dosage form is an intravenous form then the F value is termed the absolute bioavailability. In the case where the reference dosage form is another oral product, the value for F is termed the relative bioavailability.

Using plasma data

When a bioavailability study is conducted at least two dosage forms are administered to each subject. One dosage form is the product to be tested, while the other dosage form is a standard or reference dosage form. This may be an IV dose, oral solution or most commonly the original manufacturer's product. The doses are given with sufficient time between administrations for the drug to "washout" or be completely eliminated. We usually assume that each subject eliminates each dosage form at the same rate.

During the derivation of the Wagner-Nelson equations we calculated Amax, the maximum amount absorbed as:-

Amax = V * kel *

= V * kel * AUC

= F * DOSE

therefore

F =

Now by giving two dosage forms A and B, and calculating AUC values for each.

and if DOSE^A = DOSE^B and if we can assume that kel^A = kel^B and V^A = V^B then:-

Thus a relative bioavailability, F, can be calculated. If the B dosage form is given IV then F^B = 1 and F = F^A and thus F^A can be called the absolute bioavailability.

EXAMPLE:

AUC^A = 12.4 mg.hr/L [Dose = 250 mg] and AUC^B = 14.1 mg.hr/L [Dose = 200 mg