Chapter 5 Analysis of Urine Data

return to the Course index
previous | next

Plotting and Analyzing Urine Data

Cumulative amount excreted versus time

Urine data is usually collected as drug concentration in the urine sample and the volume of the sample at the end of the collection interval. Multiplying these numbers together gives the amount of drug excreted during the collection interval as ΔU. Accumulating these ΔU values gives the cumulative amount of drug excreted up to the specified time, U. We can plot U versus time as the cumulative amount excreted versus time plot. As we lose drug from the body it will appear in urine. Earlier we wrote the differential equation for U and presented the integrated equation for U, Equation 5.2.9.

The linear plot of cumulative amount excreted into urine as unchanged drug versus time is shown below. Notice that the value of U^∞ is NOT EQUAL to the dose, it is somewhat less than dose, unless all of the dose is excreted into urine as unchanged drug. The remaining portion of the dose should be found as metabolites and from other routes of excretion.

The equation for the cumulative amount excreted versus time is shown below in Equation 5.3.1.

Equation 5.3.1 Cumulative Amount excreted into Urine versus Time

This translates into the plot shown in Figure 5.3.1. Notice that the total amount excreted as unchanged drug, U^∞, is less than the dose administered in this plot.

Figure 5.3.1 Linear Plot of U versus Time showing Approach to U^∞ not equal to DOSE

Click on the figure to view the interactive graph

Cumulative amount excreted plots are basically descriptive in nature. At most, you can get a general sense of how much drug is excreted, an estimate of U^∞ and an approximate estimate of t_1/2.

Rate of excretion (R/E)

Equation 5.2.8 on the previous page represents the rate of excretion of unchanged drug into urine as an exponential function.

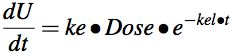
Equation 5.3.2 Rate of Excretion of Unchanged Drug into Urine

Since urine data is collected over an interval of time the data is represented as ΔU rather than dU. Also, since ΔU is collected over a discrete time interval the time point for this interval should be the midpoint of the interval, t_midpoint. Equation 5.3.2 can be replaced by Equation 5.3.3 to better represent the data collected. It may look like a strange way of plotting the data, but actually it's quite convenient to use because urine data results are collected as an amount of drug excreted during a time interval. The amount excreted is the product of the volume of urine voided and the concentration of drug in the sample. This is a rate measurement.

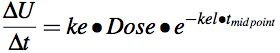
Equation 5.3.3 Rate of Excretion of Unchanged Drug versus midpoint time

Taking the ln of both sides gives Equation 5.3.4, an equation for a straight line. Plotting ln[ΔU/Δt] versus time_midpoint provides kel from the slope and ke from the intercept divided by the Dose

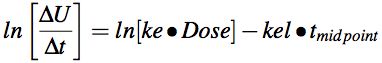
Equation 5.3.4. Natural log of Rate of Excretion versus Time

Note: The intercept (on semi-log graph paper) is ke • DOSE.

Figure 5.3.2. Semi-log Plot of ΔU/Δt versus Time_midpoint Showing Slope = - kel
with fe = 0.75, kel = 0.2 hr^-1; ke = 0.15 hr^-1

Click on the figure to view the interactive graph

Rate of excretion plots can be very useful in the determination of the parameters such as kel, ke and fe. There can be a little more scatter that with the ARE plot, below. Analysis of 'real' data may show considerable scatter in the rate of excretion plot. Thus, positioning the straight line on a semi-log plot may be difficult. In practical terms it is difficult to get a lot of early times points unless the subjects are catheterized and even then early times may be difficult to interpret. This means that this method can be difficult to use with drugs which have short half-lives. However, a significant advantage of the rate of excretion plot is that each data point is essentially independent, especially if the bladder is fully voided for each sample. A missed sample or data points is not critical to the analysis.

NOTE: This plot is rate of excretion versus midpoint of the collection interval, time.

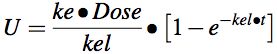
Amount remaining to be excreted (ARE)

The third plot is the amount remaining to be excreted, the ARE plot. The equation for this plot can be derived from Equation 5.3.1.

Equation 5.3.5 Cumulative amount excreted versus time

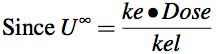
Equation 5.3.6 Total Amount Excreted as Unchanged Drug, U^infinity

Equation 5.3.5 can be rewritten in terms of U^infinity.

Equation 5.3.7 Cumulative amount excreted versus time

Equation 5.3.8 Cumulative amount excreted versus time

Rearranging Equation 5.3.8 gives Equation 5.3.9.

Equation 5.3.9 Amount Remaining to be Excreted as Unchanged Drug versus Time

Taking the log of both sides give the straight line equation. Plotting ln[U^∞ - U] versus time provides kel from the slope and U^∞ from the intercept.

Equation 5.3.10 Ln(ARE) versus time

where

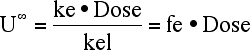
Equation 5.3.11 U^∞

Note ke and fe

Thus:

Equation 5.3.12 ARE versus time

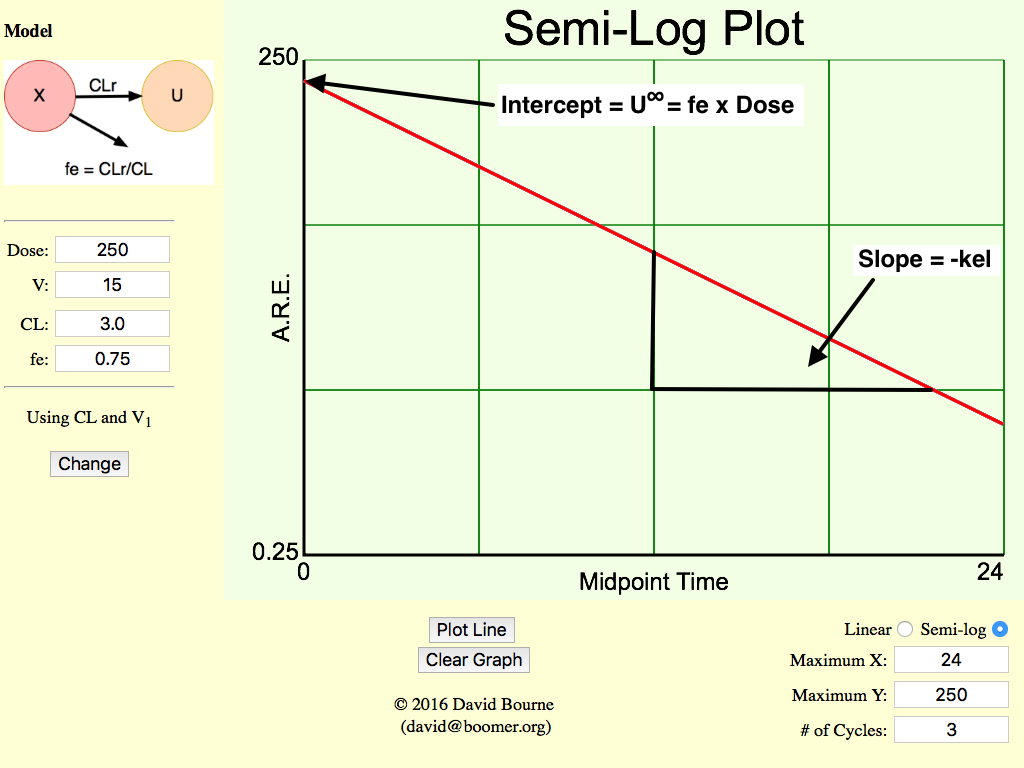
Figure 5.3.3 Semi-log Plot of ARE versus time

Click on the figure to view the interactive graph

Amount remaining to be excreted (ARE) plots use the U^∞ value to estimate each data point. Error in any data is accumulated into U^∞ and thus each ARE value. This can lead to curved lines (instead of the expected straight lines) or an inability to use the method (with a missing sample). With good data these plots may be somewhat smoother.

For practice you can use these urine data collected after an IV bolus dose and estimate pharmacokinetic parameters.

return to the Course index

This page was last modified: Sunday, 28th Jul 2024 at 4:48 pm

Privacy Statement - 25 May 2018

Material on this website should be used for Educational or Self-Study Purposes Only

Pharmacy Math Part Two
A selection of Pharmacy Math Problems