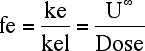
Equation 5.4.1 Fraction Excreted into Urine as Unchanged Drug
return to the Course index
previous | next
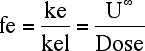
Equation 5.4.1 Fraction Excreted into Urine as Unchanged Drug
and
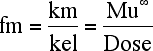
Equation 5.4.2 Fraction Excreted into Urine as a Metabolite
Equation 5.4.2 could be repeated for any number of metabolites. Note:
For example. Vancomycin fe = 0.95 (Dose 500 mg; V = 33L; Cp0 = 15 mg/L)
The normal kel = 0.116 hr-1 (t1/2 = 6 hr)
Equation 5.4.1, the equation for fe, leads to:
ke = kelnormal • fe = 0.116 x 0.95 = 0.110 hr-1
km = kelnormal • fm = kelnormal • (1 - fe) = 0.116 x 0.05 = 0.006 hr-1
If we now consider a patient with a creatinine clearance of 12 to 13 ml/min. That is, about 1/10 th of the normal kidney function, ke should then be about 1/10 of normal in this patient.
therefore
kepatient = 0.011 hr-1
Now assuming km is unchanged
| kelpatient | = kepatient + km |
| = 0.011 + 0.006 hr-1 | |
| = 0.017 hr-1 (t1/2 = 41 hour) |
Thus the half-life changes from 6 hours to 41 hours in this patient with impaired renal function. Therefore it takes seven times longer for the body to eliminate half the dose. If repeated doses were given based on a normal half-life the levels in this patient would rapidly reach toxic concentrations.
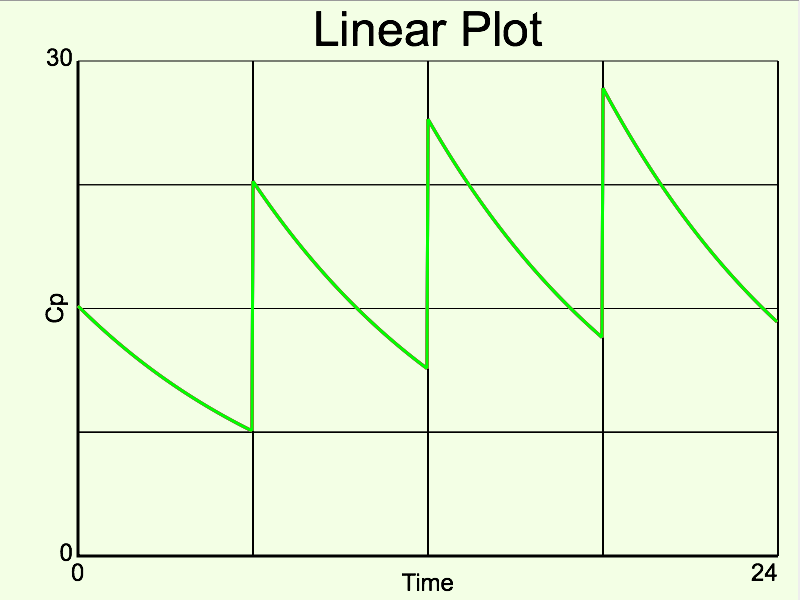
Figure 5.4.1 Plot of Cp versus Time after Multiple Doses in Patient with Normal Renal Function
Compare Figure 5.4.1 with Figure 5.4.2
Note: The Change of Scale

Figure 5.4.2 Plot of Cp versus Time after Multiple Doses
Click on the figure to view the interactive graph
kenormal = kelnormal • fe = 0.58 x 0.15 = 0.087 hr-1
km = kelnormal • fm = kelnormal • (1 - fe) = 0.58 x 0.85 = 0.493 hr-1
if the patient ke is reduced by a tenth
the kepatient = 0.009 hr-1
and again assuming that km is unchanged
| kelpatient | = kepatient + km |
| = 0.009 + 0.493 hr-1 | |
| = 0.502 hr-1 (t1/2 = 1.4 hour) |
Thus the half-life changes from 1.2 hour to 1.4 hours.
Material on this website should be used for Educational or Self-Study Purposes Only
Copyright © 2001 - 2026 David W. A. Bourne (david@boomer.org)
 | A tvOS app which presents a collection of video tutorials related to Basic Pharmacokinetics and Pharmacy Math |
|