Chapter 5 Analysis of Urine Data

return to the Course index
previous | next

Clearance

Clearance can be defined as the volume of plasma which is completely cleared of drug per unit time but this isn't always a clear explanation of this important parameter. The symbol is CL and common units are ml/min, L/hr, i.e. volume per time. One way of looking at clearance is to consider the drug being eliminated from the body ONLY via the kidneys. [If we were to also assume that all of the drug that reaches the kidneys is removed from the plasma then we have a situation where the clearance of the drug is equal to the plasma flow rate to the kidneys. All of the plasma reaching the kidneys would be cleared of drug]. The amount cleared by the body per unit time is dX/dt (here equal to dU/dt), the rate of elimination (also the rate of excretion in this example). To calculate the volume which contains that amount of drug we can divide by Cp. That is the volume = amount/concentration. This is the same as Equation 4.10.2 in Chapter 4.

Equation 5.5.1 Clearance as the Ratio of Rate of Excretion to Cp

For this particular example where elimination = excretion and kel = ke we can derive another equation for clearance which may useful.

Since

Equation 5.5.2 Rate of Excretion

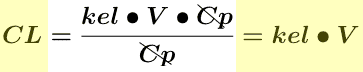
Equation 5.5.3 Clearance calculated from kel and V

As we have defined the term here CL is the total body clearance. We have assumed that the drug is cleared totally by excretion in urine. Below we will see that the total body clearance can be divided into clearance due to renal excretion and that due to other processes such as metabolism.

Clearance is a useful term when talking of drug elimination since it can be related to the efficiency of the organs of elimination and blood flow to the organ of elimination. It is useful in investigating mechanisms of elimination and renal or hepatic function in cases of reduced clearance of test substances. The units of clearance, volume/time (e.g. ml/min) may be easier to visualize, compared with elimination rate constant (units 1/time, e.g. 1/hr) although half-life (in units of time) is probably even easier. Some people view clearance as a primary pharmacokinetic parameter along with the apparent volume of distribution although both these parameters can be related to more fundamental terms.

Figure 5.5.1 Drug clearance via the Kidney

As an example if the kidney removes all of the drug presented by blood flow then the renal clearance will be equal to renal blood flow, Q_renal (= Q_kidney). In later chapters we will look at some of these more fundamental terms.

When a drug is eliminated by more than one pathway total body clearance, CL, can be separated into various clearance terms describing these pathways. Thus, total body clearance might be split into clearance due to renal excretion, CL_R and clearance due to another pathway such as metabolism, CL_M.

Equation 5.5.4 Renal Clearance from ke and V

This is a mathematical representation of CL_R. Later, in Chapter 16, we will see that renal clearance is functionally dependent on processes such as glomerular filtration rate, renal secretion and reabsorption.

and

Equation 5.5.5 Metabolic or Hepatic Clearance from km and V

Again this is a mathematical representation of CL_M. Later, in Chapter 17, we will see that liver or hepatic clearance is functionally dependent on factors such as liver blood flow, fraction of unbound drug and intrinsic liver metabolism.

Note

Equation 5.5.6 Total Body Clearance from kel and V

Clearance can also be Calculated using AUC

Another more general method of calculating clearance can be derived from the basic definition, Equation 5.5.1. For renal clearance we can write:

Equation 5.5.7 Renal Clearance

Integrating both sides gives

Equation 5.5.8 Renal Clearance Integrated Equation

Rearranging gives

Equation 5.5.9 Renal Clearance calculated from U^∞ and AUC

Hepatic or metabolic clearance can be derived in a similar fashion.

Equation 5.5.10 Hepatic Clearance calculated from Mu^∞ and AUC

Since the total amount eliminated is the IV dose (the total amount absorbed) total body clearance can also be calculated from the AUC.

Equation 5.5.11 Total body clearance Calculated from Dose and AUC

Unlike Equations 5.5.4, 5 and 6 which use model derived parameter values. Equations 5.5.9, 10 and 11 use the model independent parameters AUC and Dose, U^∞ or Mu^∞ when the disposition (distribution and elimination) parameters are linear or first-order.

Variable Renal Clearance

Equation 5.5.7 can be useful in determining if renal clearance is consistent throughout or between dosing intervals. Plotting ΔU/Δt versus Cp_midpoint for the collection interval, Δt, should provide a straight line if renal clearance is constant. If clearance is NOT constant after the drug administration dividing ΔU/Δt by Cp_midpoint provides estimates of renal clearance for each of the collection periods (Equation 5.5.1).

References

Clearance has been discussed on the PharmPK listserv.

return to the Course index

This page was last modified: Sunday, 28th Jul 2024 at 4:48 pm

Privacy Statement - 25 May 2018

Material on this website should be used for Educational or Self-Study Purposes Only

Pharmacy Math Part One
A selection of Pharmacy Math Problems