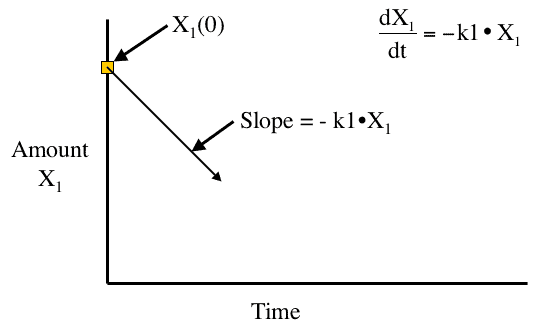
Figure 10.2.1 Linear plot of amount versus time
| Boomer Manual and Download | ||||
| PharmPK Listserv and other PK Resources | ||||
| Previous Page | Course Index | Next Page | ||

Figure 10.2.1 Linear plot of amount versus time
Euler's method is a point slope method
The point (starting point) is the initial value for the first calculation
The slope (differential equation is the result of calculating (evaluating) the differential equation value at the starting point.
Thus, for this example of a one compartment model after an IV Bolus dose;
Point = X1(0)
and Slope = - k1 • X1(0)

Figure 10.2.2 Calculation of the next data point
Thus, with X1(0) = 100 mg, k1 = 0.25 hr-1 and stepsize = 0.1 the new value is 97.5 mg. For comparison, the concentration using the exact equation of Dose • e-k1 • 0.1 = 100 • e-0.25 • 0.1 = 97.53. Not too bad, about 0.03% error.
We can extend the calculation out for as long as we like. The table below provides the calculation out for 0.5 hours.

Table 10.2.1 Table of Calculations using Euler's Method
Note the exact answer is Dose • e-k1 • 0.5 = 100 • e-0.25 • 0.5 = 88.25. An error of 0.17%.
Euler's method calculations are based on the equation for the differential equation, the slope.
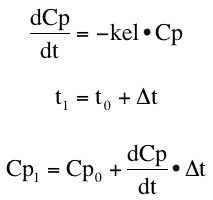
Figure 10.2.3 Equations used in Euler's Method Calculation
The equations in Figure 10.2.3 can be repeated out to what ever time is required. Remember this is a straight line approximation to a line that is usually curved. The method is only accurate if the step size is not too big. We can see this with another example. Using parameters Cp0 = 100 and kel = 0.3 hr-1 we can explore the effect of step size. In the table below either 1, 2, 4, or 10 steps are taken to get from time 0 to time 1.
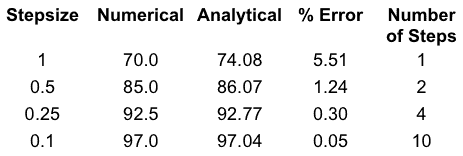
Table 10.2.2 Effect of stepsize on accuracy with Euler's method
Note the error drops from over 5 % to 0.05 % by decreasing the stepsize by 10. After 10 steps the error with the smaller stepsize would be approximately 0.5 %. A 10 fold improvement for a 10 fold increase in computational cost.
The effect of the larger stepsize, in this case 1, on the calculation is illustrated below.

Figure 10.2.4 Plot of Amount versus Time calculated exactly and using Euler's method
Notice the divergence between the slope at each time point and the exact curve, as time progresses.
Euler's method is quite straight forward and easy to program but it requires small sizes for an accurate calculations. The smaller the stepsize the large the number of steps and time and computational cost required to achieve a satisfactory answer. Other point-slope methods, such as Runge-Kutta, tend to be more efficient, giving more accurate answers with relatively fewer steps.
iBook and pdf versions of this material and other PK material is available
Copyright © 2001-2022 David W. A. Bourne (david@boomer.org)