Chapter 19 Multi-Compartment Pharmacokinetic Models

return to the Course index
previous | next

Oral Administration

Following oral administration of a drug with two compartment characteristics, Cp is described by an equation with three exponential terms.

Diagram 19.7.1 Scheme for Oral Two-Compartment Pharmacokinetic Model

The model is shown in Diagram 19.7.1.

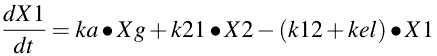
Equation 19.7.1 Differential Equation for Drug Amount in the Body after Oral Administration

Differential equation

Equation 19.7.2 Integrated Equation for Drug Amount in the Body after Oral Administration

where A + B + C = 0

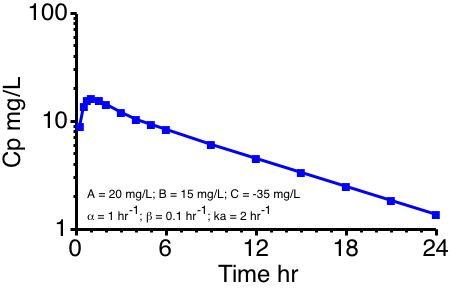
Figure 19.7.1 Semi-Log Plot Showing Pronounced Distribution

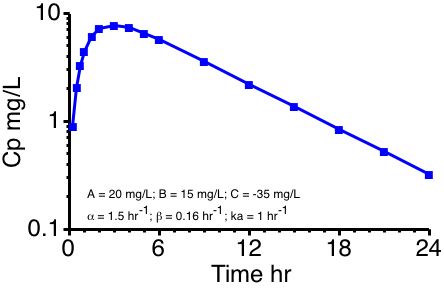
Figure 19.7.2 Semi-Log Plot Without Distribution Phase Evident

Bioavailability

Bioavailability calculations are the same as for the one compartment model, i.e., by comparison of AUC or U^∞. These apply for any linear system. Also if α, β, and ka are sufficiently separated the method of residuals can be applied (twice) to determine values for these three parameters.

Average Plasma Concentration

The average plasma concentration equation can also be used to calculate appropriate dosing regimens. For example if an average plasma concentration of 20 mg/L is required and V1 = 15 L, kel = 0.15 hr^-1, F = 0.9 and a dosing interval of 12 hours is to be used then the required dose can be calculated from the equation for Cp_average.

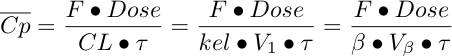
Equation 19.7.3 Equation for Average Plasma Concentration

The required dose can be calculated using Equation 19.7.3 and the data provided. Thus

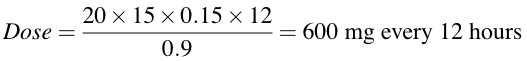
A spreadsheet to calculate Cp versus time after IV Bolus, IV Infusion (fast), IV Infusion (slow), and/or Oral can be downloaded by clicking on the figure below.

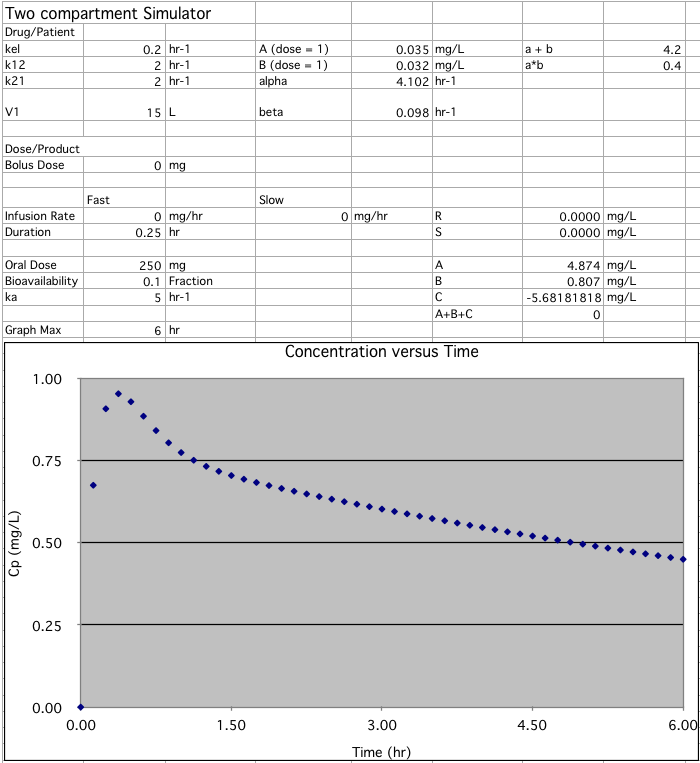
Click on the figure
to download and use the Excel spreadsheet
Spreadsheet as a Numbers^™ file

Figure 19.7.3 A Spreadsheet Illustrating Concentrations Calculated According to a Two Compartment Model

Student Objectives for this Chapter

return to the Course index

This page was last modified: Sunday, 28th Jul 2024 at 5:02 pm

Privacy Statement - 25 May 2018

Material on this website should be used for Educational or Self-Study Purposes Only

Pharmacy Math Part One
A selection of Pharmacy Math Problems