Cp_max and Cp_min equations

More useful equations can be derived from this general equation. These are equations to calculate the maximum and minimum plasma concentration after many doses. That is as n ---> and t = 0 or t = t. These are the limits of the PLATEAU CONCENTRATIONS.

Equation XIV-17 Cp Immediately after Many Doses

and

Equation XIV-18 Cp Immediately before Many Doses

An example may be helpful: t_1/2 = 4 hr; IV dose 100 mg every 6 hours; V = 10 liter

then

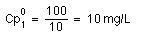
What are the Cp_max and Cp_min values when the plateau values are reached

kel = = 0.17 hr^-1

R = e^{-kel *} = e^{-0.17 x 6} = 0.35

therefore

and

therefore the plasma concentration will fluctuate between 15.5 and 5.4 mg/liter during each dosing interval when the plateau is reached.

We can now calculate the plasma concentration at any time following multiple IV bolus administration and we can calculate the Cp_max and Cp_min values.

Figure XIV-11, Plot of Cp Versus Time showing Time to Approach 50% of Plateau during Multiple Dose Regimen

Plasma Concentration versus Time Plots

• Linear
• Semi-log

In the previous example Cp_max = 15.5 mg/liter

A suitable loading dose would be Cp_max * V

155 mg as a bolus would give Cp = 15.5 mg/liter, followed by 100 mg every 6 hours to maintain the Cp_max and Cp_min values at 15.5 and 5.5 mg/liter respectively.

In general:-

The loading dose is Cp_max * V

And since

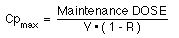
(see Equation XIV-17, page XIV-11)

Equation XIV-19 Loading Dose

or

Maintenance DOSE = Loading DOSE * (1 - R)

We can try another example of calculating a suitable dosing regimen.

Consider V = 25 liter; kel = 0.15 hr^-1 for a particular drug and we need to keep the plasma concentration between 35 mg/liter (MTC) and 10 mg/liter (MEC).

What we need is the maintenance dose, the loading dose, and the dosing interval.

Since

therefore

Also

R = e^{-kel *} = 0.2857

then

- kel * = -1.2528 or

= 8.35 hour; the dosing interval.

A dosing interval of 8 hours would be more reasonable. Thus with = 8 hr and kel = 0.15 hr^-1

R = e^{-kel *} = e^{-8 x 0.15} = 0.3012

If we use Cp_max =

Maintenance dose = Cp_max * V * (1 -R) = 35 x 25 x (1 -0.3012) = 611 mg

Again a more realistic dose would be 600 mg every 8 hours.

To check

Cp_max = = 34.3 mg/L

and

Cp_min = Cp_max * R = 10.3 mg/L

This regimen would be quite suitable as the maximum and minimum values are still within the limits suggested. All that remains is to calculate a suitable loading dose.

Loading dose = Cp_max * V = 35 x 25 = 875 mg either 875, 850 or 800 mg

This answer can be expressed graphically.

Figure XIV-11. Plasma Concentration after Multiple IV Bolus Doses

Calculate a suitable multiple IV bolus dosage regimen for specified Cp_min and Cp_max

Calculate Cp_min and Cp_max after multiple IV bolus doses

Copyright 2002 David W.A. Bourne