Chapter 6

Intravenous Infusion

return to the Course index
previous | next

Post Infusion

Before moving on we should look at the equation for plasma concentration after an infusion is stopped.

Remember that the equation for plasma concentration versus time during an IV infusion is:

Equation 6.6.1 Drug Concentration during an IV Infusion

If the infusion is continued indefinitely then the plasma concentration approaches a steady state plasma concentration.

If however the infusion is stopped the plasma concentration can be expected to fall.

Scheme or diagram

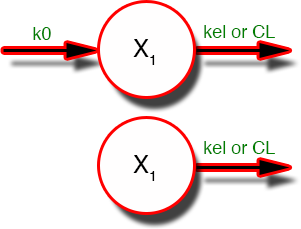
Before and After Infusion

Figure 6.6.1 During and After an IV Infusion - One Compartment Model

The scheme shown to represent 'after the infusion is stopped' is the same as that for the bolus injection.

Equations

The equation for drug concentration versus time during an IV infusion is shown above as Equation 6.6.1. At the end of the infusion period when t = D the plasma concentration can be calculated using Equation 6.6.2.

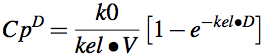
Equation 6.6.2 Concentration at the End of an IV Infusion

Once the infusion is stopped all we have is first order elimination.

Then


Equation 6.6.3 Concentration after an IV Infusion has Stopped

where t is time counted from the start of the infusion. Thus t - D is the time since the end of the infusion. Then

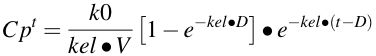
Equation 6.6.4 Concentration during and after an IV Infusion

Equation 6.6.4 can be used as shown when t is greater than D (that is for drug concentrations after the infusion has stopped). Also, if t is less than or equal to D you should set D = t before using the equation. In this way the term e-kel * (t-D) becomes equal to 1 and can be dropped from the equation and the equation reverts to Equation 6.6.1.

Figure 6.6.2 Linear Plot of Cp versus Time for Interrupted Infusion. Showing Mono exponential Rise and Fall

Click on the figure to view the interactive graph

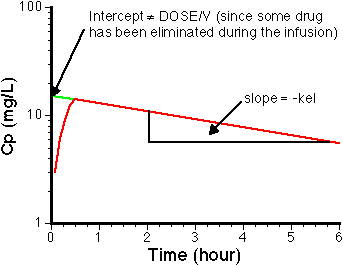
If we use the previous example data, V = 25 L; kel = 0.17 hr-1; D = 0.5 hour; and k0 = 735 mg/hr, what would be the plasma concentration be at 4.5 hours (t = 4.5 hours). That is if we stop the loading infusion and don't start the maintenance infusion.

Figure 6.6.3 Semi-log Plot of Cp versus Time. NOTE: Intercept is not Cp0

Click on the figure to view the interactive graph

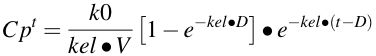
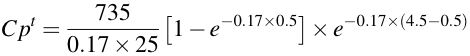
Thus 4 hours after the infusion was stopped the drug concentration has fallen to half the value at the end of the infusion. Did you remember that the drug half-life was 4 hours.

Example Calculation

Following a two-hour infusion of 100 mg/hr plasma samples were collected and analysed for drug concentration. Calculate kel and V.

Time (hr) 3 5 9 12 18 24
Cp (mg/L) 12 9 8 5 3.9 1.7

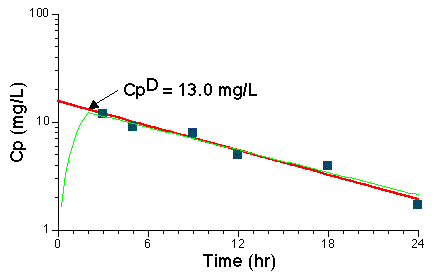
Figure 6.6.4 Plot of Cp versus Time after a Two-Hour Infusion

The red line drawn through the data points and back to the Y-axis represents the best-fit line.

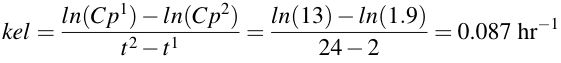
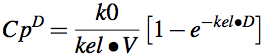
Rearranges to

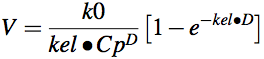
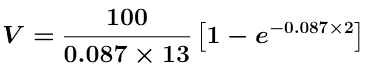
Javascript Calculators using Equation 6.6.4

Calculator 6.6.1 Calculate kel and V given post infusion Cp versus time data

Enter a value for the infusion rate and duration (< 3 hr)
Infusion rate k0 (zero order mass/time)
Infusion duration < 3 (time)
 
Cp at 4 hours (mg/L)
Cp at 5 hours (mg/L)
Cp at 6 hours (mg/L)
Cp at 9 hours (mg/L)
Cp at 12 hours (mg/L)
Cp at 24 hours (mg/L)
 
kel (first order reciprocal time)
V (volume)
Analysis of Plasma Concentration versus Time Data After IV Infusion Administration

Figure 6.5.1 Analysis of Plasma Concentration versus Time Data After IV Infusion Administration

Click on the figure to view the interactive graph

Something to consider

Item 1. Which equation should you use. That is, is the simpler IV bolus dose equation close enough or is the 'full' IV infusion equation necessary. Winter (Winter 2004) suggests using the drug elimination half-life as a criteria. That is, if the infusion duration is less than 1/6th of the elimination half-life the simpler IV bolus equation is satisfactory, within 10%. When the infusion duration is longer the more complete IV infusion equation is better.

First try simulating concentration versus time after an IV bolus: Dose = 250 mg; D = 0 hr (IV Bolus); kel = 0.123 hr-1; V = 25 L. Contrast this with an IV infusion of the same dose over an infusion duration of 1 or 2 hours. Explore the problem as a Linear Plot - Interactive graph Winter 2004.

For practice try calculating required infusion rates and parameter values. Compare your answers with the computer! These problems include bolus/infusion and fast/slow infusion regimen calculations as well as parameters determinations from two post infusion drug concentrations.

For practice try estimating various parameter values from post infusion data. Compare your answers with the computer! These problems include graphing post infusion drug concentration data on semi-log graph paper and estimating parameters from the slope and intercept of the best-fit line.

References

Student Objectives for this Chapter
Chapter 6 Crossword Puzzle and key

return to the Course index

This page was last modified: Sunday, 28th Jul 2024 at 4:49 pm

Privacy Statement - 25 May 2018

Material on this website should be used for Educational or Self-Study Purposes Only

Copyright © 2001 - 2025 David W. A. Bourne (david@boomer.org)

Pharmacokinetics cover The Book
Pharmacokinetics
This Course in ePub format		 Get it on Apple Books