Chapter 12

Physical-Chemical Factors Affecting Oral Absorption

return to the Course index
previous | next

pH - Partition Theory

For a drug to cross a membrane barrier it must normally be soluble in the lipid material of the membrane to get into membrane and it has to be soluble in the aqueous phase as well to get out of the membrane. Many drugs have polar and non-polar characteristics or are weak acids or bases. For drugs which are weak acids or bases the pKa of the drug, the pH of the GI tract fluid and the pH of the blood stream will control the solubility of the drug and thereby the rate of absorption through the membranes lining the GI tract.

Brodie et al. (Shore, et al. 1957) proposed the pH - partition theory to explain the influence of GI pH and drug pKa on the extent of drug transfer or drug absorption. Brodie reasoned that when a drug is ionized it will not be able to get through the lipid membrane, but only when it is non ionized and therefore has a higher lipid solubility.

Brodie tested this theory by perfusing the stomach or intestine of rats, in situ, and injected the drug intravenously. He varied the concentration of drug in the GI tract until there was no net transfer of drug across the lining of the GI tract. He could then determined the ratio, D as:

Equation 12.2.1 Brodie's D Value

i.e.

Equation 12.2.2 Brodie's D Value in Another Form

Figure 12.2.1 Diagram Showing Transfer Across Membrane

These values were determined experimentally, but we should be able to calculate a theoretical value if we assume that only non ionized drug crosses the membrane and that net transfer stops when [U]b = [U]g

Brodie found an excellent correlation between the calculated D value and the experimentally determined values.

Review of Ionic Equilbrium

The ratio [U]/[I] is a function of the pH of the solution and the pKa of the drug, as described by the Henderson - Hasselbach equation

Weak acids

where HA is the weak acid and A- is the salt or conjugate base

Equation 12.2.3 Dissociation Constant - Weak Acids

taking the negative log of both sides

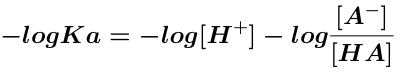
and rearranging gives Equation 12.2.4 where pKa = -log Ka and pH = -log[H+]

Equation 12.2.4 Henderson - Hasselbach Equation - Weak Acids

Explore this equation for monoprotic acid as well the equations for bi- and tri- protic acids with the graphs on the Pharmaceutics graph page.

Weak Bases

where B is the weak base and HB+ is the salt or conjugate acid

Equation 12.2.5 Dissociation Constant - Weak Acids

taking the negative log of both sides

and rearranging gives Equation 12.2.6 where pKa = -log Ka and pH = -log[H+]

Equation 12.2.6 Henderson - Hasselbach Equation - Weak Bases

or alternately

Equation 12.2.7 Dissociation Constant - Weak Base

taking the negative log of both sides

Note that Ka • Kb = [H3O+] • [OH-] = Kw which is approximately 10-14, thus pKb - pOH = pH - pKa and the equation above can be changed into Equation 12.2.6.

Table 12.2.1 Some Typical pKa Values for Weak Acids at 25 °C Martin 1993

Weak Acid pKa
Acetic 4.76
Acetylsalicyclic 3.49
Ascorbic 4.3, 11.8
Boric 9.24
Penicillin V 2.73
Phenytoin 8.1
Salicyclic 2.97
Sulfathiazole 7.12
Tetracycline 3.3, 7.68, 9.69

Table 12.2.1 Some Typical pKa Values for Weak Bases at 25 °C Martin 1993

Weak Base pKb
Ammonia 4.76
Atropine 4.35
Caffeine 10.4, 13.4
Codeine 5.8
Erythromycin 5.2
Morphine 6.13
Pilocarpine 7.2, 12.7
Quinine 6.0, 9.89
Tolbutamide 8.7

D Values and Drug Absorption

Even though the D values refer to an equilibrium state a large D value will mean that more drug will move from the GI tract to the blood side of the membrane. The larger the D value, the larger the effective concentration gradient, and thus the faster the expected transfer or absorption rate.

Figure 12.2.2 Diagram Illustrating Drug Distribution between Stomach and Blood (Weak Acid)

Compare D for a weak acid (pKa = 5.4) from the stomach (pH 3.4) or intestine (pH 6.4), with blood pH = 7.4

Stomach

Equation 12.2.8 Weak Acid from Stomach

Blood

Equation 12.2.9 Weak Acid from Blood

Therefore the calculated D value would be




Equation 12.2.10 Brodie D Value - Weak Acid (Stomach)

Figure 12.2.3 Diagram Illustrating Drug Distribution between Intestine and Blood (Weak Acid)

By comparison in the intestine, pH = 6.4

The calculated D value is (100+1)/(10+1) = 9.2

From this example we could expect significant absorption of weak acids from the stomach compared with from the intestine. Remember however that the surface area of the intestine is much larger than the stomach. However, this approach can be used to compare a series of similar compounds with different pKa values.

We have applied the pH - partition theory to drug absorption, later we will use this theory to describe drug re-absorption in the kidney.

Figure 12.2.4 Plot of ka versus fu

With this theory it should be possible to predict that by changing the pH of the G-I tract that we would change the fraction non ionized and therefore the rate of absorption.

Thus kaobserved = ku • fu assuming that the ionized species is not absorbed.

Figure 12.2.5 Plot of ka (apparent) versus fu for Sulfaethidole from Rat Stomach

Redrawn from Crouthamel, W.G., Tan, G.H., Dittert, L.W. and Dolusio, J.T.
1971 Drug absorption IV. Influence of pH on absorption kinetics
of weakly acidic drugs, J. Pharm. Sci., 60, 1160-63

For some drugs it has been found that the intercept is not zero in the above plot, suggesting that the ionic form is also absorbed. For example, results for sulfaethidole. Maybe the ions are transported by a carrier which blocks the charge, a facilitated transport process.

Calculator 12.2.1 Calculate the D Value for a Weak Acid
Starting with 100 units of a WEAK ACID

  Drug pKa    
  [HA]GI
 
GI pH  
 
Total - GI
 [A-]GI
[HA]Blood
  
 
  Blood pH
 
[A-]Blood
 Total - Blood
%U
%I
D Value 		%U
%I

Calculator 12.2.2 Calculate the D Value for a Weak Base
Starting with 100 units of a WEAK BASE

Drug pKa   Drug pKb  
  [B]GI
 
GI pH  
 
Total - GI
[HB+]GI
[B]Blood
  
 
  Blood pH
 

[HB+]Blood		 Total - Blood
%U
%I
D Value 		%U
%I

Some items to consider

Item 1. A series of drugs, weak acids, have been developed. The best five drugs in the series have measured pKa values of 3.4, 4.7, 5.4, 4.2 and 5.1. Which drug has the highest D value in the stomach (pH 2.5)? Which drug would be better absorbed from the small intestine (pH 7.2).
Item 2. A series of drugs, weak bases, have been developed. The best five drugs in the series have measured pKa values of 10.4, 9.7, 9.4, 8.2 and 8.7. Which drug candidate has the highest D value in the stomach (pH 2.5)? Which drug would be better absorbed from the small intestine (pH 7.2).

A few more (related) interactive graphs

Monoprotic figure
Monoprotic Species versus pH		 Monoprotic figure
Biprotic Species versus pH
Monoprotic figure
Triprotic Species versus pH		 pH Rate Profile
pH Rate Profile
References

return to the Course index
previous | next

This page was last modified: Sunday, 28th Jul 2024 at 4:55 pm

Privacy Statement - 25 May 2018

Material on this website should be used for Educational or Self-Study Purposes Only

Copyright © 2001 - 2025 David W. A. Bourne (david@boomer.org)

Pharmacy Math 2 coverPharmacy Math Part Two
A selection of Pharmacy Math Problems		 Get it on Apple Books