
Figure 2.8.1. Linear Plot of Cp versus Time showing AUC and AUC segment
return to the Course index
previous | next
Toxicology AUC can be used as a measure of drug exposure. It is derived from drug concentration and time so it gives a measure how much - how long a drug stays in a body. A long, low concentration exposure may be as important as shorter but higher concentration. Haber's law propose exposure k = C X t (Fritz Haber, 1868-1934) where k is essentially AUC. Some drugs are dosed using AUC to quantitate the maximum tolerated exposure (AUC Dosing). The efficacy of some antibiotics are related to AUC/MIC, thus maintaining a concentration above a minimum inhibitory concentration (MIC) is more important than peak concentrations.
Biopharmaceutics The AUC measured after administration of a drug product is an important parameter in the comparison of drug products. Studies can be performed whereby different drug products may be given to a panel of subject on separate occasions. These bioequivalency or bioavailability studies can be analyzed by comparing AUC values.
Pharmacokinetics Drug AUC values can be used to determine other pharmacokinetic parameters, such as clearance or bioavailability, F. Similar techniques can be used to calculate area under the first moment curve (AUMC) and thus mean resident times (MRT).

Figure 2.8.1. Linear Plot of Cp versus Time showing AUC and AUC segment
The area under the plasma concentration time curve (AUC) is very useful for calculating the relative efficiency of different drug products (We'll talk about this later, see Chapter 9). It can used to calculate the total body clearance (CL) and the apparent volume of distribution.
If we have a smooth line for concentration versus time or an equation for Cp versus time from a pharmacokinetic model we could slice the area into vertical segments. Each segment would be very thin, Δt and in extreme dt, in width (much smaller than the segment in Fig 2.8.1). The total AUC is calculated by adding these segments together. In calculus this would be the integral. Each very narrow segment has an area = Cp • dt. Thus the total area (AUC) is given by Equation 2.8.1:
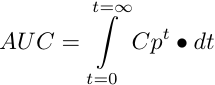
Equation 2.8.1. Total AUC calculated from Very Narrow Segment
With a first order elimination process the integrated equation for plasma concentration as a function of time is:
Equation 2.8.2. Cp versus Time after an IV Bolus dose
This is essentially the same as the integrated equation (Equation 2.6.3) we demonstrated for amount of drug remaining (which can be derived using Laplace transforms). The difference here is concentration not amount. We can substitute this equation for Cpt into Equation 2.8.1 to derive an analytical equation for AUC:

Equation 2.8.3. AUC calculated as the integral of Cp versus time
From Math Tables we would find that:

At t = 0, e-k•t = 1 and at t = ∞, e-k•t = 0
Therefore:

OR

Equation 2.8.4. AUC Calculated from Concentration and k
This is analytical integration (exact solution, given exact values for Cp0 and k). This only applies for concentrations collected after an IV bolus and first order kinetics.
Also, after most dosage regimens, once the concentration follow a semi-log linear straight line we can use a similar equation to calculate the remaining AUC. The AUC of the last segment. With t = t to ∞, AUC is calculated as Cpt/k. We will use this result further down on this page
This can be derived as:

OR

Equation 2.8.5 AUC from t to infinity
We could use Equation 2.8.4 to calculate the AUC value if we knew Cp0 and k but usually we don't do this. We calculate AUC directly from the Cp versus time data. We need to use a different approach. The simplest, most common approach is a numerical approximation method called the trapezoidal rule.

Figure 2.8.2. Linear Plot of Cp versus Time showing Typical Data Points
We can calculate the AUC of each segment if we consider the segments to be trapezoids. [Four sided figure with two parallel sides].
The area of each segment can be calculated by multiplying the average concentration by the segment width. For the segment from Cp2 to Cp3:
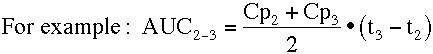
This segment is illustrated in Fig 2.8.3 below.

Figure 2.8.3. Linear Plot of Cp versus Time showing One Trapezoid
The area from the first to last data point can then be calculated by adding the areas together.
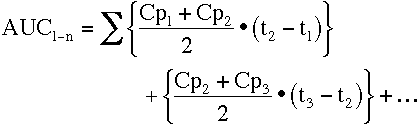
Equation 2.8.6 AUC from Cp 1 to Cp n
Note: Summation of data point information (non-calculus)
This gives:

Figure 2.8.4. Linear plot of Cp versus time showing areas from data 1 to data n
To finish this calculation we have two more areas to consider. The first and the last segments.
After a rapid IV bolus with a one compartment model, the first segment can be calculated after determining the zero plasma concentration Cp0 by extrapolation. That is, by plotting the Cp versus time data on semi-log graph paper and extending the best-fit line back to the y-axis.
Thus

Equation 2.8.7 AUC from Cp 0 to Cp 1
If we assume that the last data points follow a single exponential decline (a straight line on semi-log graph paper) the final segment can be calculated from the equation above from tlast to infinity:

Equation 2.8.8 AUC from tlast to infinity
Thus the total AUC can be calculated as:
 |
|
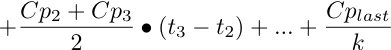 |
Equation 2.8.9 Total AUC from time zero to infinity
In the case of an IV administration, one compartment model there is only one slope on semi-log graph paper and thus only one rate constant, k. With other modes of adminstration and other pharmacokinetic models multiple rate constants may be represented in the concentration versus time curve. However, if the last few data points approximate a straight line on semi-log graph paper, representing the slowest rate constant this can be used to calculate the last AUC segment from the time of the last data point to infinity. In Chapters 8 and 9 there are two rate constants, ka and kel. Either rate constant may be the slowest and therefore used to calculate the last AUC segment.
where k is the slower rate constant. In Chapter 19 there are two rate constants after IV administration, α and β. By definition β is less than α so the last AUC segment would be calculated using this rate constant.
After oral administration there are three rate constant, α, β and ka. Beta or ka could be the slowest rate constant and used in the calculation of the last AUC segment. In each case it is the slowest rate constant that is used in the calculation of the AUC for the last segment.
|

|
||||||||||||||||||||||||||||||||||||||||||||
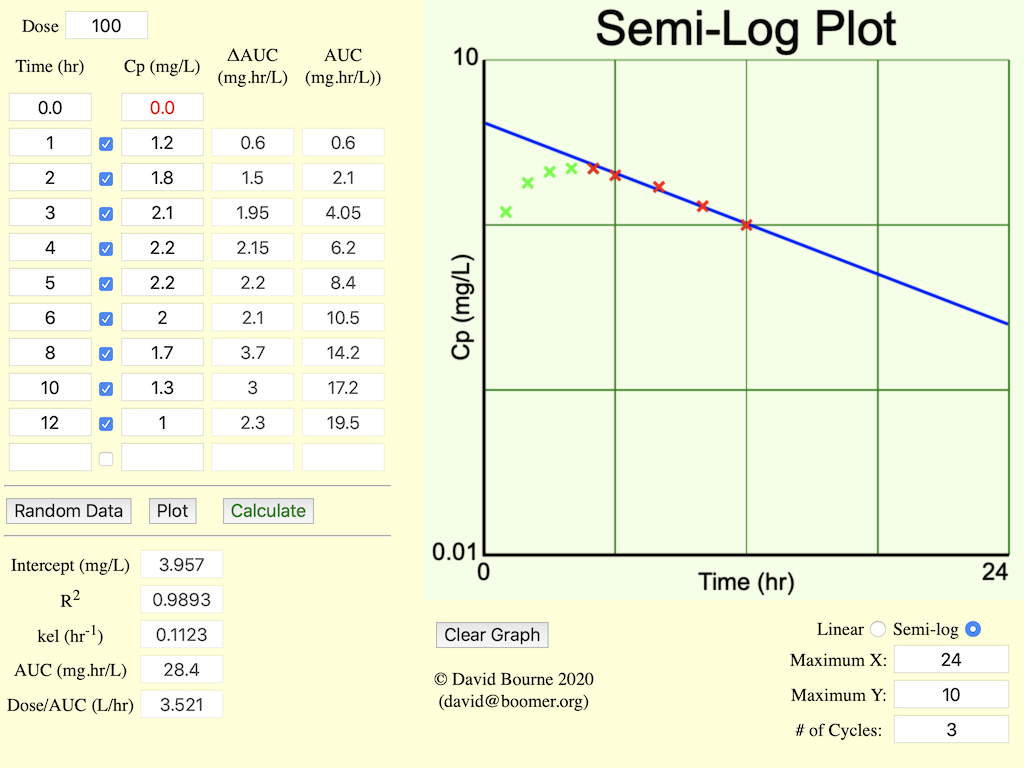
Figure 2.8.5 Calculation of AUC from Cp versus Time Data
Click on the figure to view the interactive graph
Material on this website should be used for Educational or Self-Study Purposes Only
Copyright © 2001 - 2026 David W. A. Bourne (david@boomer.org)
 | A tvOS app which presents a collection of video tutorials related to Basic Pharmacokinetics and Pharmacy Math |
|