Chapter 14

Loading Dose and Maintenance Dose

return to the Course index
previous | next

Loading Dose and Maintenance Dose

The IV bolus loading dose to quickly achieve a required drug concentration, Cpmax, can be calculated as Cpmax • V

Loading dose from V and Cp(max)

Equation 14.6.5 Loading Dose

Rewriting Equation 14.6.2 with Dose expressed more explicitly as the Maintenance Dose.

Equation 14.6.6 Cpmax

Maintenance dose

Equation 14.6.7 Maintenance Dose

or

Maintenence dose

Equation 14.6.8 Maintenance Dose

In the previous example Cpmax was 15.5 mg/liter

A suitable loading dose can be calculated as Cpmax • V = 15.5 x 10 = 155 mg as a bolus which would give Cp = 15.5 mg/liter. This loading dose could be followed by 100 mg every 6 hours to maintain the Cpmax and Cpmin values at 15.5 and 5.5 mg/liter, respectively.

Using Cpmax and Cpmin to Calculate a Suitable Dosing Regimen

We can try another example of calculating a suitable dosing regimen. Consider that we know V = 25 liter and kel = 0.15 hr-1 for a particular drug and for this drug we need to keep the plasma concentration between 35 mg/liter (MTC) and 10 mg/liter (MEC).

What we need is the maintenance dose, the loading dose, and the dosing interval.

Dividing Equations 14.6.2 by Equation 14.6.3

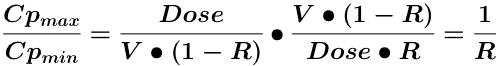
Equation 14.6.9 Cpmax and Cpmin provides 1/R

therefore

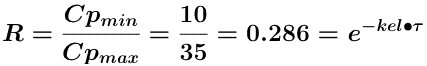
taking the ln of both sides

Solving for Τ gives

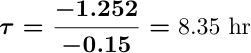
A dosing interval of 8 hours would be more reasonable and keeps the concentration between the limits of MTC and MEC. Thus with τ' = 8 hr and kel = 0.15 hr-1

From Equation 14.6.6

Equation 14.6.10 Maintenance Dose

Maintenance dose = 35 x 25 x (1 - 0.301) = 612 mg

Again we can round the value to a more realistic value, a maintenance dose of 600 mg every 8 hours.

This regimen should be quite suitable as the maximum and minimum values are still within the limits suggested. All that remains is to calculate a suitable loading dose.

This loading dose could be round (down) to a more suitable 850 or 800 mg. Let's use 800 mg.

The dosing regimen is then a loading dose of 800 mg followed by a maintenance dose of 600 mg every 8 hours. To check this regimen

Concentrations from the loading dose

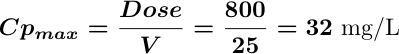
NOTE the use of the loading dose in this equation and that the Cpmax is below the MTC.

Concentrations from the maintenance dose

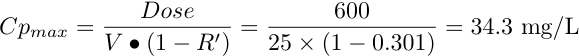
and

Here we use the maintenance dose. Note, the Cpmax and Cpmin are below and above the MTC and MEC, respectively.

This answer can be expressed graphically.

Figure 14.6.2 Plasma Concentration after Multiple IV Bolus Doses

Calculator 14.6.1 Calculate a suitable multiple IV bolus dosage regimen for specified Cpmin and Cpmax

Patient (weight Kg) is to receive a drug by multiple IV bolus doses. For optimal treatment drug concentration should be kept between Cpmax mg/L and Cpmin mg/L. This drug has an apparent volume of distribution of L/Kg and an elimination rate constant of hr-1 (Clearance = L/kg.hr).

First calculate the dosing interval, tau.

Tau hour.

Enter a new (rounded) value for tau. hr.

The next step is to calculate a suitable maintenance and loading dose.

Start with a loading dose of mg as an IV Bolus and a maintenance dose of mg as an IV Bolus every hour.

Calculator 14.6.2 Calculate Cpmin and Cpmax after Multiple IV Bolus Doses

Patient (weight Kg) has received mg of a drug as an IV Bolus every hours. This drug has an apparent volume of distribution of L/Kg and an elimination rate constant of hr-1 (Clearance = L/kg.hr). Calculate the Cpmin and Cpmax at steady state.

Cpmin mg/L

Cpmax mg/L

Practice problems involving Cpmax and Cpmin at steady state after uniform multiple dose IV bolus doses. Another practice problems involving Cpmax and Cpmin at steady state after uniform multiple dose IV bolus doses. A third practice problems involving Cpmax and Cpmin at steady state after uniform multiple dose IV bolus doses.

Other practice problems involving the calculation of Cp at three times during a uniform dosing interval with Linear or Semi-log graphical answers or calculation of Cp at three times during a non-uniform dosing interval with Linear or Semi-log graphical answers.

return to the Course index

This page was last modified: Sunday, 28th Jul 2024 at 4:59 pm

Privacy Statement - 25 May 2018

Material on this website should be used for Educational or Self-Study Purposes Only

Copyright © 2001 - 2025 David W. A. Bourne (david@boomer.org)

Drug Structures
Drug Structures
A game to aid recognizing drug structures
See how many structures you can name before you run out of lives
 Download from the App Store